Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
hydromechanics
1. Series 21. Year - 2. save the bubble!
Batyscaphe Trieste dived into deep sea and released a bubble which started to come to the surface. What is the vertical speed of the bubble? How will this speed change? How long it will take to reach surface? What size of bubbles will be fastest?
Úlohu vymyslel Jano Lalinský.
6. Series 20. Year - E. blowing experiment
Measure what is the maximum pressure (and underpressure) which can be made by your mouth by blowing and sucking air.
O ruce vás chtěl připravit Michael Komm.
5. Series 20. Year - 4. Buffalo Bill and Jessie James
Buffalo Bill is searching for Jessie James, well known bandit. Finaly he found him and in town Clay County they meet in fighting. Buffalo noticed a barrel full of petrol located in between both of them on a trolley. But how to get barrel near to Jessie (to light it up)?
Jessie made a hole in the barrel with his gun in 9/10 of height and the petrol is flowing from the barrel. Buffalo hits the barrel exactly in the middle and shoots again. Calculate what is the acceleration of the barrel and trolley at the beginning and how it depend on the position of the second hole from Bill's revolver. Assume the mass of bullet is negligible.
What height is optimal for petrol to splash to longest distance?
Znovu zadaná úloha V.1 z 18. ročníku, protože tehdejší řešení je špatně. Přílepek od Honzy Hradila.
4. Series 20. Year - 1. shopping for mineral water
You may remember buying plastic bottle of your favourite drink in supermarket. The bottle placed on the belt starts spinning trying to stay on the spot. Why this happen?
Analyse following situation: the bottle in rest is placed on the belt perpendicularly to the direction of belt movement.
Suddenly the belt starts moving at constant speed $v=10\;\mathrm{cm}/s$. What will be the speed of the bottle. First analyse following idealisations: (1) approximate bottle by a solid cylinder, (2) the bottle is full of liquid water which does not like to be turned. For simplicity assume negligible viscosity, then include viscosity to your calculations.
Úlohu vymyslel Jano Lalinský na nákupu v TESCU.
2. Series 20. Year - 1. Cenek's saw mill
Cenek's saw mill is located at the junction of rivers Vydra and Kremelna in the Boheminan forest (mountains). The saw mill is named after wood retailer Cenek Bubenicek, who has built in 19th century. There is water power plant at its former place declared by state as technical monument.
Power plant uses difference of water levels above and under turbine 10 m, electrical output of power station is 96 kW. Water is distributed to the turbine using rectangular open-top canal. Its width is 1 m, and water is 1,5 m deep. The estimated water speed at the middle of surface is 1 m\cdot s^{− 1}. What is the estimated efficiency of water power station?
Vymyslel Honza Prachař, když byl na výletě na Šumavě.
2. Series 20. Year - 2. crushing impact
Find a relation between the speed of meteorite (just before impact) and radius of created crater.
Na problém narazil Honza Prachař při psaní textu Fyzikální olympiády.
2. Series 20. Year - E. waves on the water
Using dimension (unit) analysis find the relation for the speed of waves on the water surface. Verify the theoretical relation and find unknown constants from measuring the speed of waves dependent on wavelength. Do not forget that there are two types of waves – one caused by gravitational field and second by surface tension.
Úloha napadla Honzu Prachaře při čteni Feynmanoých přednášek z fyziky.
2. Series 20. Year - P. shaking the tea
Explain why the tea in the box after it is shaken is separated such that larger pieces of tea leaves are on the surface. The solution can be enhanced using your observation.
S úlohou přišel Petr Sýkora.
1. Series 20. Year - P. tree height
Estimate the height of the trees on the planet. Think over all possible aspects influencing the height of the trees.
Úlohu navrhla Zuzka Safernová.
5. Series 19. Year - 1. what a stability of a ship
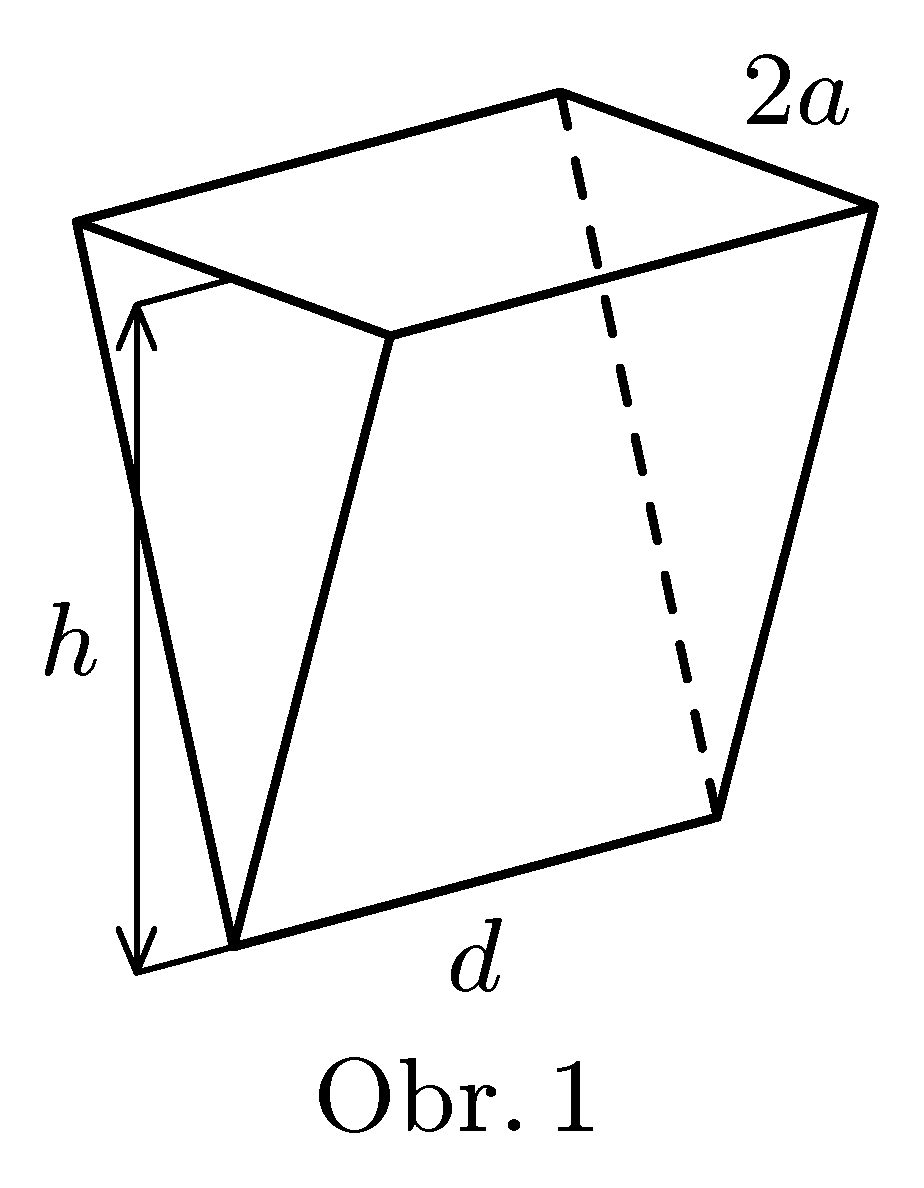
Scientists in NASA discovered special sediments of vegetable origin at Europa (Jupiter's moon). They are suitable for making very strong planks of oblong shape or triangular shape and are ideal for building a ship of height $h$, length $d$ and width 2$a$ (see figure 1) Help: captain to decide for which range of densities of ocean it is safe to sail such boat.
Assume that planks have constant thickness and density $ρ_{m}$ and that the ship is hollow and has a deck. (discuss the case when the ship is not hollow and has constant density $ρ_{m}.)$ It is not necessary to show just one final equation, more important is practical recipe (including all required equations) how to make such calculations. Try to make it simple to understand and explain all approximations made.
Vymyslel Pavel Brom při vzpomínce na historku o jedné nešťastně navržené lodi.