Search

Trains, as it is commonly known, don't have a differential and so when they go through a turn the wheels must turn with the same angular velocity. Now assume that the wheels have a cylindrical shape. Thus when going through a turn one wheel has to go a longer path than the other. The axis will have torsion applied on it and in a certain moment the frictional force between the wheel and railway rail won't be large enough and one wheel will slip and the tension on the axis will fall to 0. Determine the distance the individual slippages between depending on the radius of $R_{z}$. The wheel has a raidus of $R$, the axis has a radius of osa $r$, the length of the axis is $L$, the elastic shear modulus of the axis is $G$ (steel), wagon with $N$ wheels has a mass of $M$ and coefficient of static friction between wheels and rails$f$. Finally you can insert realistic values.

Hint: For torsion of the$φ$ cylinder of radius $R$, length $l$ and elastic shear modulus $G$, on which we apply the momentum $M$, it is true that

$$\varphi=\frac{2Ml}{G \pi R^4}$$

Consider a swing held up by two ropes of length $l=1.5\;\mathrm{m}$ that hang from a pole of radius $r=4\;\mathrm{cm}$. The child sitting on the swing shall gain in the bottom dead center such a speed $v_{0}$ that the child shall accomplish a whole turn around the horizontal pole and that the ropes shall be experiencing a tension sufficient enough for them to be rigid throughout the turn. At the same time we wish to minimalize the initial velocity. Determine the difference of the angular velocity $ω_{1}of$ the swing with the child after its return to the bottom dead point and the initial angular velocity $ω_{0}$.

Hint: To calculate the centripetal acceleration you may assume that locally the child is moving on a circular path.

A poor hungry coyote wants to catch the devilish Road Runner and he prepared the following trap to snare him: onto a sturdy rope he fastened a 500 ton anvil and he shall throw it over a branch so that it would hang over the road and he will wait. How many times does he need to make the rope go around the branch so that he can hold it there just using his own weight? Assume that the weight of the rope is negligible compared to the weight of the coyote.

Let us have an inclined plane on which we place a ball and we give it kinetic energy so that it will begin rolling upwards without slipping. Measure the relationship between the velocity of the ball and time and determine the loss of energy as a function of time. The inclined plane should have an angle of at least $α10°$ with the horizontal. Do not forget to describe the parameters of your ball.

What is the minimal length of a wire so that if you hang it from a ceiling, it will break due to its own mass? The wire's density is $ρ=7900\;\mathrm{kg}\cdot \mathrm{m}^{-3}$, it has a diameter $D=1\;\mathrm{mm}$, and it breaks at $σ_{max}=400MPa$. Assume that everything takes place in a homogeneous gravitational field $g=9.81\;\mathrm{m}\cdot \mathrm{s}^{-2}$.

Bonus: If the wire's length is maximal possible so that it does not break, how much will it stretch (in percents)? Young's modulus of the wire's material is $E=200GPa$.

Let us consider the following model of a baseball player hitting a ball. Baseball bat is a thin homogeneous rod of length $L$ and mass $m$. The bat can only rotate around an axis perpendicular to the axis of the bat that is located at its end. The bat is rotating with an angular velocity $ω$. How far from the end of the bat should the player hit the ball in order to minimize the force with which the bat acts on the player's hands?

A loaded falling balloon will eventually reach certain constant terminal velocity. Measure how does this velocity depend on the balloon size, and on the mass of its load.

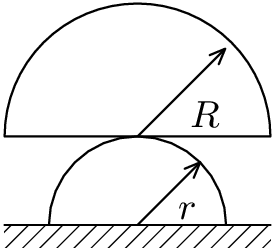
Two half cylinders are lying on top of each other as shown in the picture. The radius of the smaller one is $r$ and that of the larger one is $R$. Given $r$, what is the condition on $R$ so that the system is stable?

Bonus: If the parameters are chosen so that the system is stable, what will be the period of oscillations of the top half cylinder after it has been slightly shifted from the equilibrium position?

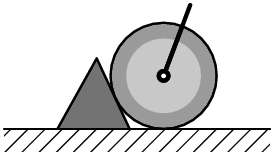
A block of wood or other material placed in front of a wheel is often used to prevent an airplane from moving (see picture). Can such a locking device prevent an airplane from moving even if its engines are on and producing maximal power? Analyze this problem and show how does the answer depend on the material of the wheels, the ground, and the locking device. Will your answer change if the height of the locking device is such that the point of contact with the wheel is at its very top?

Given that the Earth is 81 times heavier than the Moon, and that its surface gravity is 6 times greater than that of the Moon, calculate the ratio of the volumes of these two objects.