Search

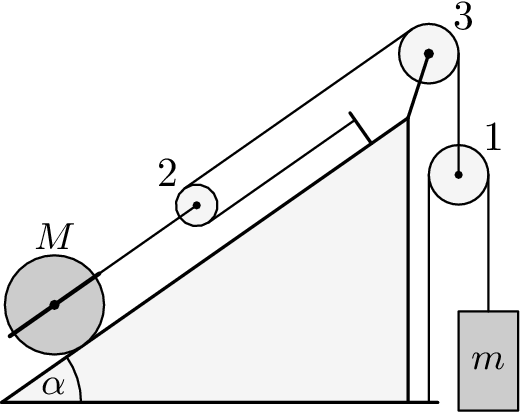
Consider the pulley system in the picture. If the masses $m_{i}$, radii $R_{i}$, and moments of inertia $J_{i}$ for all pulleys, mass $m$ of the weight, and mass $M$, radius $R$, and moment of inertia $J$ of the cylinder are all known, we neglect the weight of pulley 2 and thus consider the ropes leading to pulley 2 as parallel with the inclined plane, the coefficient of friction (both static and kinetic) between the cylinder and the surface is $f$ and the rope does not slip on the pulleys, determine the acceleration (optionally the angular acceleration as well) of the weight $m$ and the cylinder $M$.

Measure as many characteristics of a high-vis snap band as you can. We are specifically interested in:

• The band contains a piece of metal on the inside, which can be bent lengthwise (when coiled) or along the shorter edge (when straight). What are the radii of curvature of these bents if there is no external force?
• If the band is straight and we start bending it in one place, at what angle will it snap into the bent state? At what angle does it become straight again? (Do we see any hysteresis?)
• What is the torque required to bend the band?
• Is one of the states (bent or straight) more energetically favourable? Estimate by how much. Unfortunatelly, we are unable to mail these bands abroad, we therefore ask that you obtain one yourself and include pictures of the band you used in your solution.

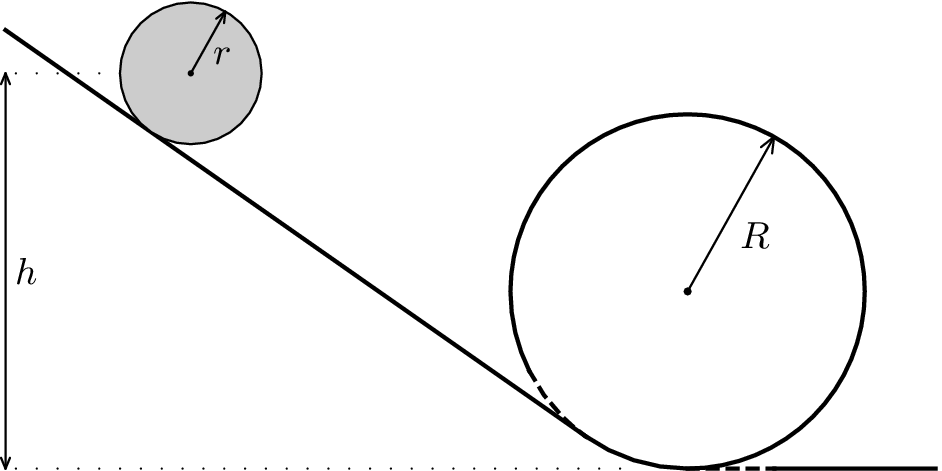
We have a plane inclined at an angle $α$ which is smoothly connected to a loop of radius $R$. What is the minimal initial height $h$ where we have to place a ball of radius $r$ (comparable to $R$, but smaller), so that the ball will roll through the loop? The ball must be always in contact with the plane or the loop and we assume that the ball does not slip.

Imagine the motion of a homogeneous ball: it starts with translation (without rotation) and gradually transitions to rolling (without slipping). Determine the time of the transition from pure translation to rolling without slipping. Consider different radius, mass, initial speed and coefficient of friction of the ball.

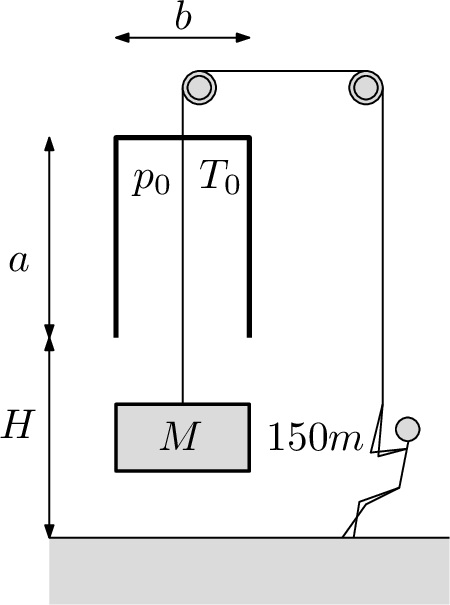
Ancient Egyptians could build a gate, but they hadn't invented the portcullis yet so they closed the gate with nilans (limestone blocks). There are 150 slaves of mass $m=60\;\mathrm{kg}$, who are at the moment slowly opening a gate closed with a nilan of mass $M=8t$. The nilan fits precisely (air-tightly) into a structure above the gate whose inner dimensions are $a=3\;\mathrm{m}$, $b=0.5\;\mathrm{m}$ and $c=3\;\mathrm{m}$. The original pressure inside the structure is $p_{0}=100kPa$ and the original temperature is $T_{0}=300K$. The structure is situated at high $H=3\;\mathrm{m}$ above the ground. Find out how high are the slaves able to lift the nilan, using only their own weight if the air temperature stays constant.

There is a sphere with inhomogeneous distribution of density on an inclined plane. We know the angle of inclination of the plane $α$, the radius of the sphere $R$ and the distance $t$ of the centre of mass from its geometrical centre. If we label the centre of the sphere $S$, the point of touch with the plane $D$ and the centre of mass $T$, then we can define the angle $φ_{0}=∠DST$ as the initial angle (before any motion begins). We also know that the centre of mass is situated in a plane given by the line segment $DS$ (the normal to the inclined plane) and the down-sloping direction. Considering all the parameters given, carefully describe the time evolution of the sphere's state of motion. The sphere does not slip.

There are two identical blocks with the mass $m$ and one of the sides of lenght $lon$ a horizontal plane. The distance between the closest two faces is 2$x_{0}$. Suddenly we start pouring water between them with the volume flow $Q$. At two sides of the blocks there is a barrier keeping the water in the place between the two blocks. The coefficient of static friction between the block and the plane is $f_{0}$ and the of the kinetic friction is $f$. There is no friction between the barriers and the blocks. What is the condition for $f_{0}$ that would keep the blocks in place? In the case of sufficiently small $f_{0}$, determine the acceleration of blocks as a function of position and also the distance, where the blocks eventually stop moving. Consider all the movement of the water reasonably slow, for any eddies to appear, for any heating of the water solely from its movement to take place or for any significant kinetic energy possesion. For the same reason of very slow $Q$, we can approximate there is no contribution of adding any water past the point where the blocks started moving. Bonus: Find a condition for turning the block over.

The notebook of a size of A4 (297 x 210 mm) lies on a desk with an inclination of $α=5°$. The notebook weights $m$, between the desk and the notebook there acts a static friction force with coefficient $f_{0}=0.52$. Then, we hit the desk so it starts to oscillate (in the direction of the inclination of the desk) with a frequency $ν=10\;\mathrm{Hz}$ and an amplitude $A=1\;\mathrm{mm}$.

• Determine by which extra force (perpendicular to the desk) we have to act on the notebook so it does not start to move.
• Determine how long it takes the notebook to fall off the desk if at the beggining its bottom edge (the shorter one) is at the bottom edge of the desk. Dynamic friction coeficient is $f$, consider notebook as a rigid plate.

One of the offices of lord Vetinari has a circular layout with a perimeter $R$ and is placed on bearings, thanks to which it can turn around its axis. To ensure maximum rotation it uses an engine that can apply any moment of force. During the turning the room has a torque of friction acting on it $M_{0}$, independent of speed, which is equivalent to the static friction torque. The chair for visitors is positioned so that a person will feel the rotation only if it will exceed $ε_{0}$. Determine what is the smallest time it will take to turn by 180°, so thatthe visitor won't notice and what is the work required to achieve it. The mass of the room, that can be approximated to a homogeneous disc, is $m$.

Bonus: Assume that the visitor will feel the roation only if the change in angular acceleration is greater than $j_{0}$.

• Assume a pen of length 10 cm with a center of mass precisely in the middle and $g=9.81\;\mathrm{m}\cdot \mathrm{s}^{-2}.Now$ imagine that you put the pen on the table with a null deviation $δx$ with an accuracy of $ndecimal$ places and with a null velocity. How long after making the pen stand can you be sure with just $n-decimal$ places of the nullness of the displacement?

• Consider a model of weather with the biggest Ljapun's exponent $λ=1.16\cdot 10^{-5}s^{-1}$. The weather forecast stops being useful if its error becomes bigger than 20 %. If you had determined the state of the weather with an accuracy of 1 %, how long do you estimate that your forecast would be good for? Give the answer in days and hours.

• Take Lorenz's model of convection from the last part, copy the function $f(xi,t)$ amd simulate and draw the values of the parameters $X(t)$ for two different trajectories using the commands X01=1;

Y01=2;

Z01=5;

X02=…;

Y02=…;

Z02=…;

nastaveni = odeset('InitialStep', 0.01,'MaxStep',0.1);

pocPodminka1=[X01,Y01,Z01];

reseni1=ode45(@f,[0,45],pocPodminka1,nastaveni);

pocPodminka2=[X02,Y02,Z02];

reseni2=ode45(@f,[0,45],pocPodminka2,nastaveni);

plot(reseni1.x,reseni1.y(:,1),reseni2.x,reseni2.y(:,1));

pause()

</pre> Instead of three dots $X02,Y02,Z02you$ have to give the initial conditions for the second trajectory. Run the code for at least five different orders of magnitude that are all still small and note the time, in which the second trajectory shall differ qualitatively from the first(ie will go in the opposite direaction). Don't decrease the deviation under cca 10^{$-8}$, because then the imprecision's of numerical integration start to show. Chart the dependency of the ungluing time on the order of magnitude of the deviation.

Bonus: Attempt to use the gained dependency of the ungluing time on the size of the deviation estimate Ljapun's exponent. You will need more than five runs and you can assume that at the moment of ungluing it will always overcome some constant $Δ_{c}$.