Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
electric current
(4 points)5. Series 27. Year - 4. Trianglular resistor
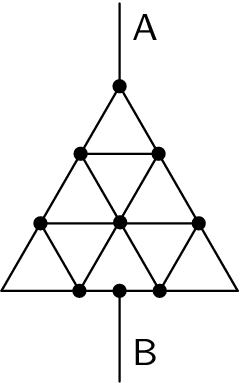
Determine the resistance of a triangle created out of resistive wires between clamps A a B, that you see in the picture. One side of the small triangle (of which the bigger triangle is composed of) has the resistance of $R_{0}.Neglect$ the resistance of the wires that led it there.
Karel was drawing triangles
(4 points)2. Series 27. Year - P. Temelínská
Estimate how much nuclear fuel get used by an atomic powerplant to generate 1 MWh of electrical energy that people use at home. Compare it with the usage offuel in a thermal powerplant. Don't forget to think about all posible ways that energy gets lost.
Bonus: Include the energy that is required to transport the fuel into your solution.
Karel přemýšlel nad ČEZem.
(4 points)1. Series 26. Year - 3. geography for physicists
Imagine that there are wires along all lines of latitude and longitude. These wires are connected at each point where they cross. Given that the resistance of one meter of this wire is $ρ$, calculate the resistance of this network between the nodes located at the North and South pole. Assume that the angular distance of neighboring lines of latitude/longitude is 15$°$.
Bonus: What would be the resistance between two nodes located on the equator and opposite of each other?
Honza dreamed of an around the world trip.
4. Series 23. Year - P. Resistance
Do think of resistance of a flowing electrolyte. Is it dependent on the direction of the flow of the electric current? Try to evaluate the difference if there is any.
by hit Grepe
6. Series 22. Year - 1. resistance
Calculate the resistance of $n-dimensional$ cube between two most distant corners (with coordinates ( 0$,0,…,0)$ and ( 1$,1,…,1))$. The cube consists only from its edges (1-dimensional objects). Try to start with 3-dimensional cube and expand in higher dimensions.
Přednesl Lukáš Ledvina
4. Series 22. Year - P. save the physics
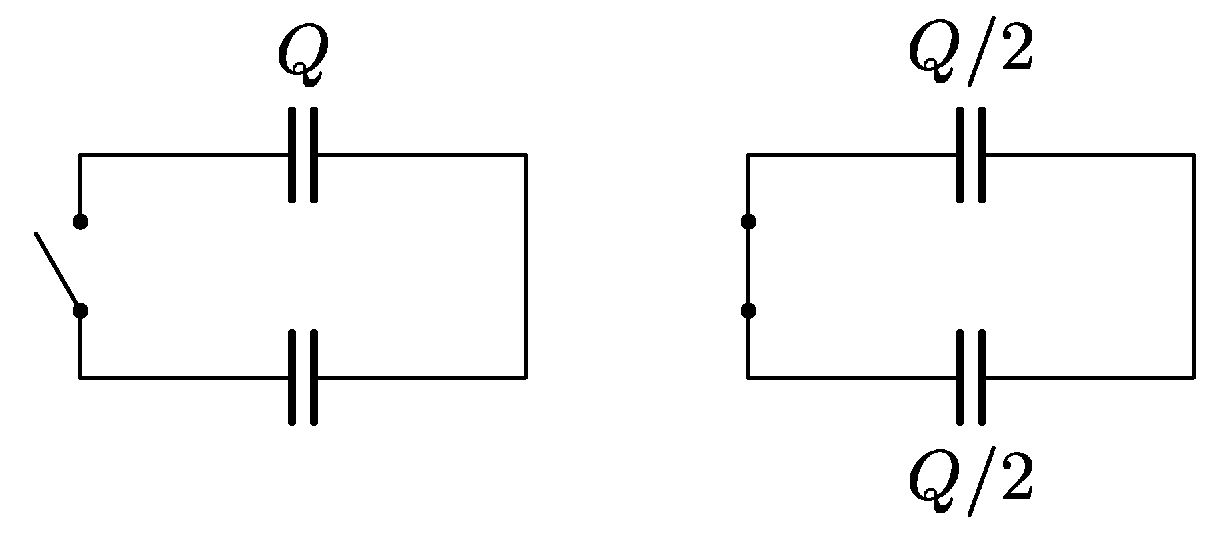
Disconnected electric circuit on the picture contains one uncharged and one charged capacitor (charge $Q)$. Wires are ideal with no resistance, both capacitors are identical. Total energy of electrical charges in circuit is then $Q⁄2C$. If the charges on capacitors become equal, then total energy will be $Q⁄8C+Q⁄8C=Q⁄4C$, which is half comparing to the beginning. Explain what happened and where the half of energy was used up. The switch is made in such way, that you can assume the energy loss has happened somewhere else.
S touhle záludností přišel Jarda Trnka.
3. Series 21. Year - S. wandering of a sailor, pi-circuit and epidemic in Prague
Integral
Integrate using Monte Carlo method function e^{$-x}$ on interval [ $-100,100]$. Try numerically find value of this integration interval from −∞ till +∞.
Hint: Function is symmetrical in origin, therefore it is sufficient to integrate on interval [ 0, +∞ ) . Make substitution $x=1⁄t-1$, where you change limits of integration from 0 to 1.
Wandering of sailor
Drunken sailor stepped out onto pier of length 50 steps and wide 20 steps. He goes to land. At each step forward looses balance and makes one step left or right. Find, what is probability of reaching land and what is probability of falling off the pier into the sea.
Sailor was lucky and survived. However the second night he goes (again drunken) from ship to land. This time there is strong wind of speed of 3 m\cdot s^{−1}, which causes change of probability of stepping to the left to 0.8 and 0.2 to the right. Again, find the probability, that he reaches the other side or will fall into the sea.
Third night the situation repeats again. The wind is blowing randomly, following normal distribution with mean value 0 m\cdot s^{−1} and dispersion 2 m\cdot s^{−1}. Find the probability of sailor reaching land. You can assume, that sailor walks slowly and inertia of wind is negligible, therefore wind is uncorrelated between individual steps.
Pi-circuit
Having 50 resistor of resistance 50 Ω we want to create a circuit with the resistance in Ohms closest to number π. Solve it using simulated annealing.
For this task you can adapt our program, which can be found on our web pages.
If you do not feel like solving this problem, try to solve problem of „traveling salesman“ with introducing curved Earth surface into a model and find solution for concrete set of towns, e.g. capitals of European countries.
Epidemic in Prague
Investigate evolution of epidemic in Prague. Assume 1 million inhabitants. Intensity of infection $β$ is 0$,4⁄1000000$ per day, cure $γ$ is ( four days )^{$-1}$. At the beginning there is 100 infected people. Compare the evolution with case of vaccinated population of 20% of population. Also compare with vaccination during the epidemic, where 0.5% population is vaccinated per day. The end of epidemic is, when less than 20 people are ill.
There is a lot of data you can get from computer simulation. Apart from the mean value also plot a graph, where you will show five random simulations. You can also observe fluctuations. Compare your results with deterministic model which does not assume randomness of process of infection. The number of points, which we will give out will reflect how many interesting data you will process.
Zadali autoři seriálu Marek Pechal a Lukáš Stříteský.
6. Series 20. Year - 3. the square the Joker
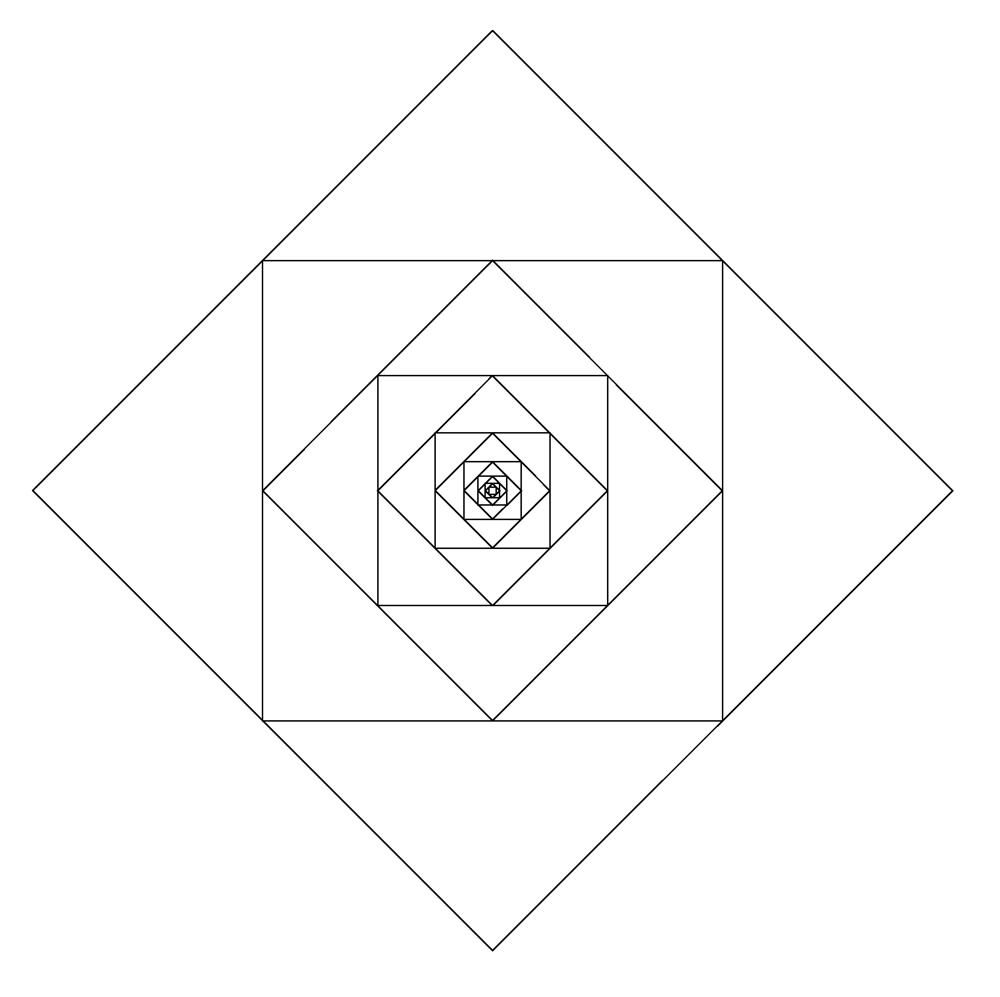
The electric circuit in the image is made from the infinite number of wire-frame-squares. The next square is exactly sqrt(2) smaller then the previous. The resistance of used wire is $R$ per one side of the largest square. What is electrical resistance between most left and most right point?
Úlohu vymyslel Marek Pechal.
2. Series 18. Year - 2. how many wires at the poles?
How many phases there have to be to allow the effective voltage between phase and ground will be the same as between two neighbouring phases?
Úlohu navrhl Pavel Augustinský.
2. Series 18. Year - 4. desperate shipwrecked people
Shipwrecked people at the north pole are trying to make a cup of coffee. Advice them, how to boil the water, to get as much as possible if there are only 3 ways how to boil it:
- Re-chargeable battery of internal resistance $2R$ is connected directly to the heating element of resistance $R$.
- The same battery is connected in series in with heating element and capacitor. Each time, when the capacitor is fully charged, it is disconnected and connected into the circuit in reverse polarity.
- The same battery will be used to charge capacitor and then the capacitor powers up by the heating element.
Vymyslel Matouš Ringel, když si na výletě vařil kávu.