Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
mechanics of a point mass
3. Series 18. Year - S. Langrange's equations first type
- Lets have a mass point suspended on massless string. Introduce Cartesian coordinates and write down equation for the mass point.
- Write Lagrange's equations of first type for mass point from part a). Show, that they are equivalent with the equation for mathematical pendulum
d^{2}$\varphi/dt^{2}$ + $g/l$ \cdot sin $\varphi$ = 0,
where $\varphi$ is angular displacement from equilibrium.
- Small body is in rest at the top of the hemisphere and starts to slide down. Using Lagrange's equations for first type calculate the height when the body take-off the hemisphere. (
Hint: The body takes-off when the $λ$ = 0.)
Autoři seriálu.
2. Series 18. Year - P. unexpected obstacle
The driver of the car moving at the speed $v$ suddenly recognise, that is heading to the middle of the concrete wall of the width of $2d$ and is in distance of $l$ from the wall. The coefficient of the friction between the tyres and the surface of road is $f$. What is the best way to do to avoid the inevitable accident. Decide, what is the maximum velocity to avoid the crash.
Napadlo Pavla Augustinského při cestě autem.
2. Series 18. Year - S. Newton's kinematics equations
- Write down and solve the kinematics equation for mass point in gravitation field of the Earth. The orientation of the coordinate system make that $x$ and $y$ are horizontal and z is vertical, pointing upwards. The starting position is $\textbf{r}_{0} = (0,0$,$h)$, starting velocity is $\textbf{v}_{0} =(v_{0}\cosα,0,v_{0}\sinα)$.
- The man with the gun sits in the chair rotating alongside vertical axe at frequency $f=1\;\mathrm{Hz}$. With the chair also the target is rotating (it is fixed to the chair). Then the man shoots the bullet at the speed of $v=300\;\mathrm{km} \cdot \mathrm{h}^{-1}$ from the rotational axes directly to the middle of the target. In what place the bullet is going to go through the target. Solve in non-inertial system and from the inertial system. The distance to the middle of the target from the centre of rotation is $l=3\;\mathrm{m}$, the air friction is negligible.
- State the dependence of the speed of the mass point at its position in gravitational field of the Sun.
Zadal Honza Prachař.
1. Series 18. Year - 1. duck on the pond
The duck is floating in the middle of the round pond. It wants to join others, unfortunately there is a fox on the bank. The duck cannot take of from water. It can take of only from the ground. Calculate the minimum ratio of the speeds of the duck and the fox for duck to be able to reach the bank and take off and not be eaten by fox. Suggest suitable strategy to reach this goal.
Někdo řekl Lence.
1. Series 18. Year - 2. pendulum
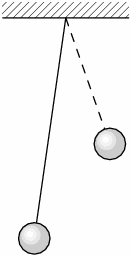
Small ball is hanging at the end of mass-less string and oscillates around equilibrium (see figure) at frequency $f$. What will be its frequency $f'$ if the length of the string is half of original length?
MFO Kanada.
1. Series 18. Year - S. kinematics of point mass
* The position of point mass in time in Cartesian coordinates is described by position vector $\vect{r}(t) =(R \cos\(\omega t\)$,R sin\(\omega t\),d)\,.$$ Calculate, what is time dependence of vectors $v(t)$ and $a(t)$. Calculate tangential, normal and bi-normal component of acceleration.
- A wheel of radius $R$ rolls without slipping at straight track at velocity $v$. A point is connected with the wheel at the distance $r$ from the centre of wheel. Calculate its movement and the velocity as function of the time in coordinate system connected with the Earth. Can the speed be zero at some moment?
Autoři seriálu.