Search

This series of questions is dedicated to the research on the „planet of the balloons“.

This year balloons are competing in the 'The higher, the better' competition. Each balloon has a piece of string attached to measure his height. All balloons have the same parameters and noone of them have won yet.

The length density of string is 11 lufts per sprungl, density of atmosphere is 110101 lufts per cubic sprungl and the radius of each balloon is 10 sprungls and weight of balloon is 10 lufts. Every object in gravitation field of the planet increases its speed by 111 sprungls per temp. Calculate the maximum height which the referees will measure and how the balloon will move after reaching this height. Unlifted part of the string is laying freely on the ground. The competition happens at low altitudes, where density of atmosphere is approximately constant.

Hint: Sprungl, luft and temp are units used on planet of the balloons. Each balloon has maximum of 1 string attached.

In tram at rest the pen is suspended on a sting of length $l$. The mass of the pen is $m$. The tram accelerates with constant acceleration $a$. Calculate the maximum angle of displacement of the pendulum (maximum angle between the string and the vertical direction) and the time when it crosses the starting position.

An engine with 8 carriages each of mass 40 t is accelerating to maximum speed of 120 km ⁄ h at the rails long 1 km. What must be the minimum weight of the engine to accelerate without wheel spinning over the rails?

Assume the static friction coefficient $f=0,2$. Air friction is negligible.

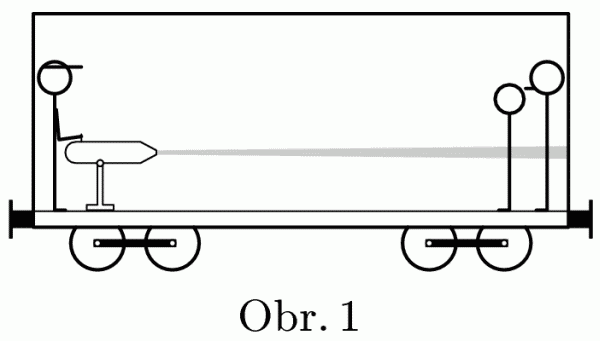
Imagine special anti-hooligan railway carriage equipped with a water cannon. The carriage weight is 30 t. Police (on the left) sprinkled hooligans with 1000 litres of water over 1 minute. How far had the carriage moved, if the wagon length is 30 m?

Assume that the carriage has brake off and that the water can escape only in vertical direction. The change in mass of carriage caused by escaped water can be neglected.

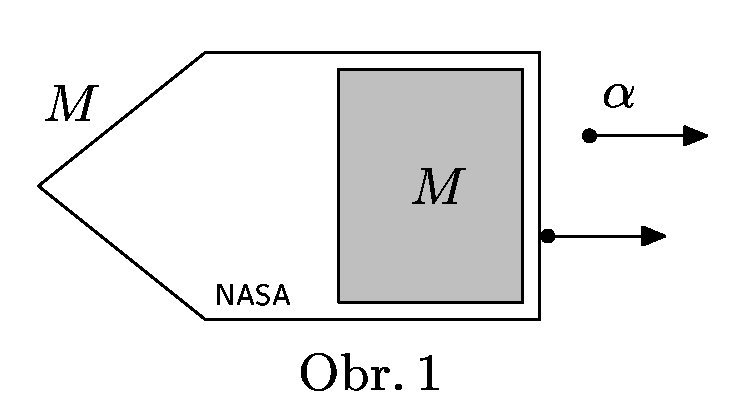
In Jet Propulsion Laboratory in California, U.S.A. in NASA laboratory the new rocket engine is under development. It uses momentum of $α-particles$ created during radioactive decay of fermium $^{257}_{100}Fm_{157}$, which mass is $m_{Fm}$ and half-life $T$. The second product is californium $^{253}_{98}Cf_{155}$. The mass of $α-particle$ is $m_{α}$, the mass of californium is $m_{Cf}$, and during the decay the energy $E$ is released. Assume, that each $α-particle$ leaves rocket in the same direction.

The space probe with above engine is in rest at the beginning and its mass is $M$, the mass of 'fuel' is also $M$. Calculate the speed of the probe $v$ after half of the fermium decays. Resulting speed calculate also for the following numerical values $E=1,106\cdot 10^{-12}J$, $M=4\;\mathrm{kg}$ a $T=100,5days$, for other values consult your table-book.

Lagrangian of a particle in electromagnetic field is

$L=\frac{1}{2}mv-qφ+q\textbf{v}\cdot \textbf{A}=\frac{1}{2}\;\mathrm{m}\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,

where $φ$ is electrical potential and $\textbf{A}$ is magnetic vector potential.

• Calculate generalized momentum of the particle $p_{i}$ belonging to the speed $v_{i}$.
• Write Hamiltonian function (in variables ($x_{i}$, p$_{i})!)$.
• Solve Hamiltonian equation, if when $\textbf{A}=**0**$ and $φ=-Ex_{1}$.

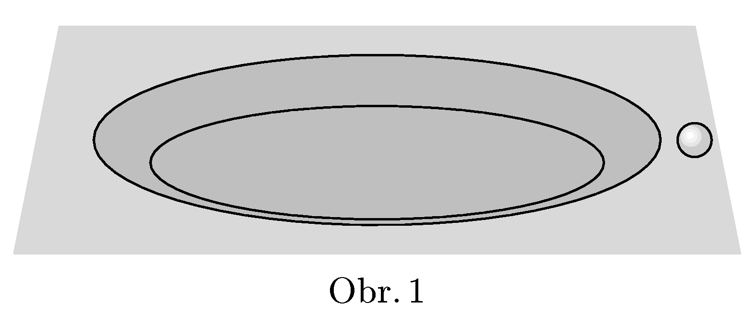
Karel is playing with a ball. While rolling it on the floor is comes to he inclined plane, which serves as a staircase, and starts to slide down. The ball is moving in such direction, that the vector of its velocity $\textbf{v}$ and the top edge of the inclined plane shows and angle $φ$. Calculate a vector of the velocity $\textbf{v}′$ of the ball under the inclined plane (its magnitude and the direction), if the height of the plane is $h$. The friction is negligible, assume that the top edge is smooth so the ball will always follow the surface.

As a bonus: what is the difference of the direction of the ball falling into a cylindrical hole of radius $R$ and the depth $h$ with inclined sides (see figure 1). The length of the inclined wall can be neglected with respect to the overall size of the hole.

The following questions will test the knowledge from all presented chapters about mechanics – Newtons formalism, D'Alembert's principle and Lagrange's formalism.

• Imagine planet Mercury orbiting around Sun. It is know, that its elliptic trajectory is rotating, the position of perihelion is moving, which cannot be explained by gravitation force.

$\textbf{F}=κ(mM\textbf{r})⁄r^{3}$.

Proof, that adding an additional central force

$\textbf{F}=C(\textbf{r})⁄r^{4}$,

where $C$ is suitable constant, full trajectory (ellipse) will rotate at constant angular speed. In other words, that exists a frame rotating at constant speed, where the trajectory is an ellipse. Knowing this angular speed $Ω$, calculate the constant $C$. Is such correction for gravitation enough?

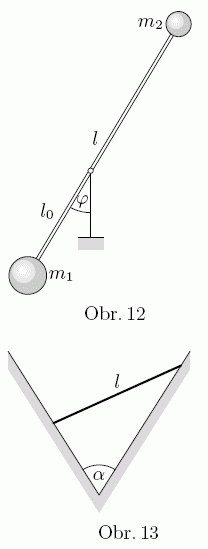
• Calculate equilibrium position of homogeneous rod of length $l$ supported by inner wall of excavation in the V-shape (see figure 12) as a function of the angle of V-shape $α$.
• Using Lagrange's equations calculate period of small oscillations of double-reverse pendulum in image 13. The weight are at the ends of weightless rod of the length $l$ and have masses $m_{1}$ and $m_{2}$, the distance from the joint from the weight $m_{1}$ is $l_{0}$.

One winter afternoon the soviet generals were out of patience while watching imperialistic West and pressed The Red Button to fire nuclear bomb. Immediately after that the young lieutenant entered the room admitting the error in calculation of the rocket's trajectory. Instead to the New York the racket was aiming to the friendly Cuba.

Luckily enough, another rocket is ready and can be sent to shoot down the first one and avoid disturbance in between socialistic countries. The original rocket was fired at the speed $v$ under the angle $α$. What angle $β$ should be set for the second rocket to shoot down the first rocket if the time delay between the launches is $T$.

Discuss when the peace between socialistic countries can be saved and when not. And of course everyone knows, that the Earth is flat and the gravitation field is homogeneous.

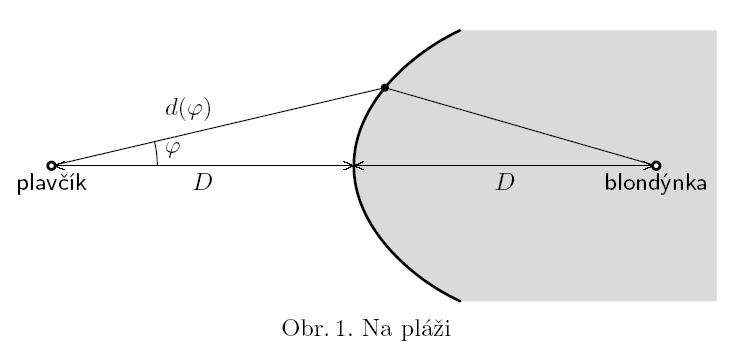
The lifeguard (plavcik) is standing in distance $D$ from the beach. He suddenly sees drowning blond girl (blondynka) which is in distance $D$ in sea (see fig. 1). The lifeguard can run at maximum speed $v$ and swim at maximum speed $v/2$. The distance from the lifeguard to the beach end is defined by following equation

$$d(\phi) = \frac{D}{3}( 8\cos{\phi}- {2\sqrt{16\cos^2{\phi}-12\cos{\phi} -3}}-3)\,,$$

where φ is angle blond-lifeguard-beach. What is the optimum trajectory for the lifeguard to safe her?