Search

Jakub has a spinning top with a spiral drawn on its upper side. He lets the top spin and watch it from above. What does he see and why?

Two travelers, one fat and the other skinny, are arguing who would have better chances of surviving in extreme conditions. Tell them who will live longer in the following environments. Hot(50 °C), cold(-1 °C), after a boat accident in the Mediterranean sea, inside a hurricane, inside a heavy snow storm and in the middle of earthquake inside a city. Except of their body fat they are exactly the same. They even wear the same clothes and they do not carry anything else. Be original and remember that details matter.

The wagon fort stands on the inclined plane (elevation angle is $α)$. The wagons are of the same weight, the distance between adjacent ones is $s$ and their total number is $N$. All of them have their brakes on at the beginning. Cunning Hetman Žižka sets the brakes of the uppermost wagon off and the wagon starts to accelerate. On the way down it hits other wagons (when the impact occurs, the wagon which was hit sets its brakes off immediately and continues to run down the slope together with the one which hit it). Calculate the velocity of the wagon fort after the last impact. Bonus: task: Calculate the distribution of weight of wagons in order to achieve constant velocity after each impact.

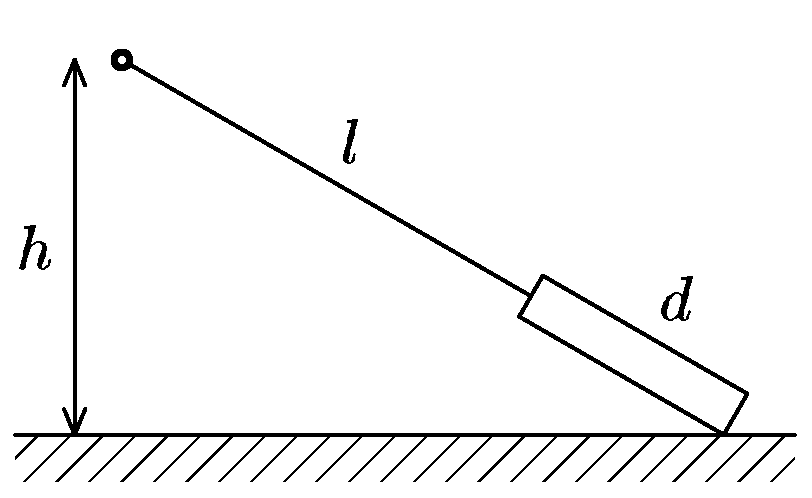
A cord of length $l$ = 1.5 m is tied to a fixed point at height $h$ = 1 m. There is a plank of length $d$ = 0.5 m attached at the end of the cord so that the cord is stretched; the cord and the plank lie in the same line (see picture). On releasing the ties, the plank will slide along its edge before touching the ground with the surface of its bottom side. Then it will move in the direction opposite to the friction force with the friction coefficient $f$. Determine the value of the coefficient so that the plank’s side attached to the cord stops reaching the projection of the fixed point defined beforehand.

It is a well-known fact that an asteroid hits the Earth on its way around the Sun (it is moving in the same plane as the Earth does) December 21, 2012. Suppose that the asteroid’s orbit is an ellipse with the following parameters: lengths of the transverse (major axis) and conjugate (minor axis) diameter are 4 AU and 0.5 AU respectively. People were far too busy to start solving the problem before December 1, 2012. What is the trajectory that needs to be used by a brave world authority to unleash a nuclear warhead to avert the end of the world?

Kryštof set on a journey by train and fell asleep. When he woke up in a tunnel, he felt that there is a force dragging him to a side. Although the train was lit up, he could not see outside. He remembered that the train track is tilted at corners. He realised that even though he remembers the original direction of the train he has no clue as to the direction of the corner taken. In other words, he cannot tell the difference between left-turning train being sufficiently slow, the resultant force directed towards the centre of the corner and the right-turning train being fast enough, the resultant force directed out of the corner. Suggest an experiment to help Krystof solve the problem. The more propositions you submit, the more points you get.

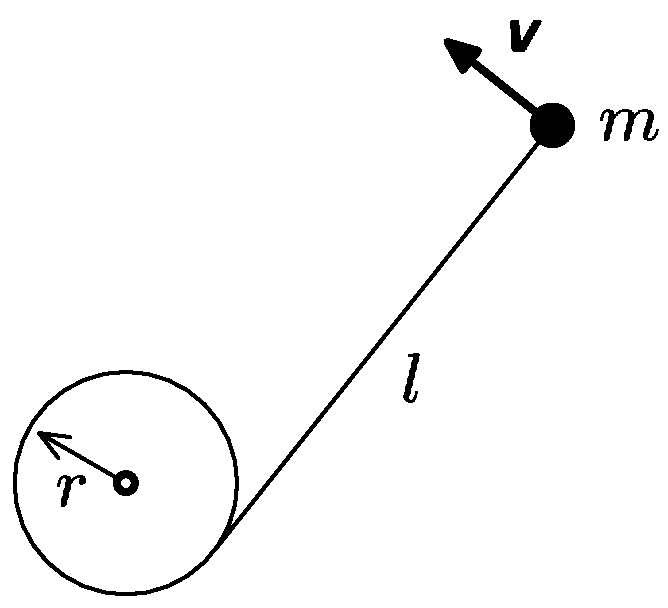
There is a weight of mass $m$ tied by a cord of length $l$ to a stake of radius $r$ put in the ground. The cord is taut and the weight lies on the ground. Lukas kicks the weight orthogonal to the cord so that it has a velocity of $v$. The cord starts to wrap around the stake. Calculate the necessary change in the coefficient of Coulomb friction between the weight and the ground in function of weight’s distance from the stake so that the velocity remains constant.

Terka jumps from one-metre high wall. At the beginning, she has her arms stretched and raised above her head. She lowers her arms during the fall. How much does it change her velocity at the moment of hitting the ground? First, make a qualified guess as to mass, acceleration, velocity of Terka’s arms as well as other body parameters. Second, solve the problem.

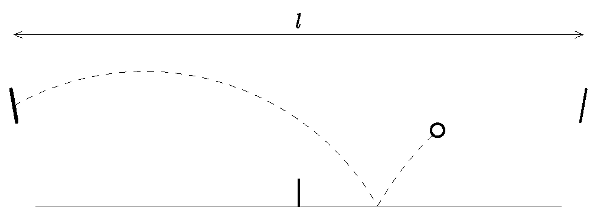
Mr. Broucek (from children fairy tale) was followed up by Etherea, which is closest to the mass point. After having ordered pork and cabbage, Mr. Broucek tried to deprive her by imprisonement between two fixed table tennis bats. The distance between bats was $l$ and both were turned at an angle, and Etherea was jumping between them as table tennis ball so that it always re-bounced the same height. To make torturing more realistic, he put a net of the height of $h$ at the centre. Mr. Broucek is a clever wag, so he wanted to (as in ping-pong) on each ball (=Etherea) crossing that the ball would touch the ground Calculate the frequency with which, depending on all sorts of parameters (rotation bats, initial ball speed, angle, …) Etherea flies, and when this frequency is highest. Assume that the motion happens in plane and the reflections from obstacles (from the Moon or from the bat) is just the opposite as the speed, all movements happen take place in vacuum.

Build a long domino line and measure the speed of falling wave. For known dimensions of domino bricks and variable distance between them. Will the speed stabilise?