Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
mechanics of rigid bodies
3. Series 19. Year - 1. cylinder touching sphere
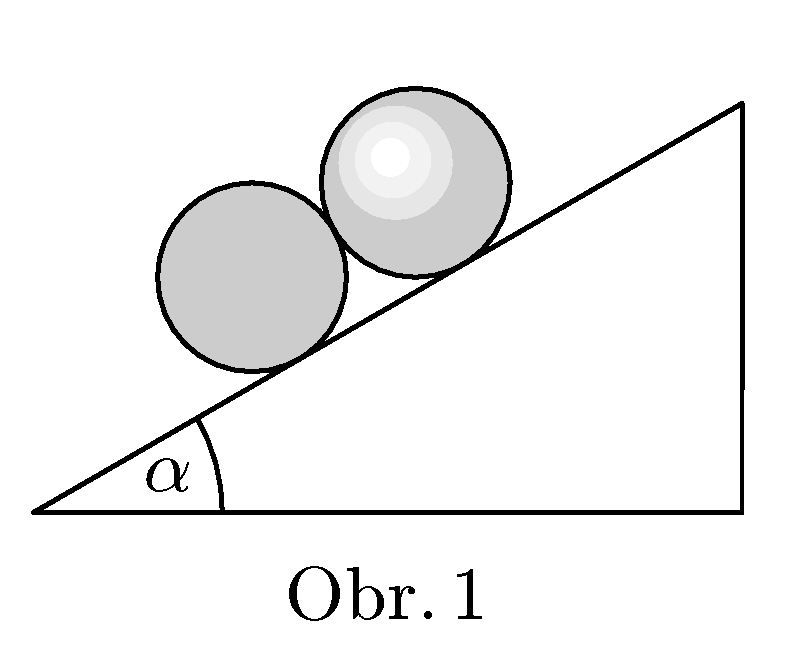
A cylinder and a sphere, both of the same radius and same weight are placed on inclined plane and are touching each other (see fig. 1). Determine, at which condition they will stay in rest.
Řešil Petr Sýkora při TJUFu.
1. Series 19. Year - 3. Armageddon
Alarm! Red lights indicate fatal threat. The meteoroid of know cross-section $S$ is approaching toward the Earth. Its thermal capacity is $c$. Calculate the increase of meteorite temperature during the flight through the atmosphere.
Assume, that its speed gets constant before impact and that it is heating uniformly. Estimate the part of energy which is used for heating the air in the atmosphere. Is this model realistic? Decide, if the meteorite will have higher or lower temperature if flying through the vacuum instead of air (vacuum has zero heat capacity).
Upravená úloha Kájinkova padajícího kulového kladívka.
1. Series 19. Year - E. hardness of balls
When you play marbles on autumn day, borrow few marbles and throw them against hard and flat surface. Then make a mark in the height where marble reached and measure it. From the measured values calculate coefficient of bounciness (ratio of energy before and after rebound).
Similar method is used for sorting hard/soft ball bearings. Soft balls do not bounce over barrier and are disposed.
Lenka
6. Series 18. Year - 4. non-stoppable walker
Lets go back to Olympic games in Athens and determine maximum theoretical speed of the race walker. The walker is disqualified, if every referee (observer) agrees, that at least one leg was touching the ground in every moment.
Kdo jiný, než Matouš.
4. Series 18. Year - 2. following the string
A small cylinder of radius $r$ and mass $m$ is rolling on the inclined plane. At the end of the plane it follows smoothly to horizontal motion and starts to wind onto itself string of the linear density $ρ$. At what distance from the end of inclined plane will the cylinder stop? You know the height of the inclined plane $h$ and it slope $α$. The friction is negligible.
8. ročník 1.kolo
3. Series 18. Year - P. the tower from push-carts
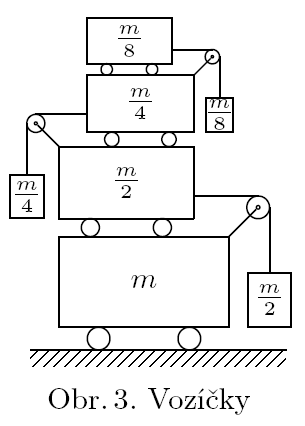
What is the acceleration of the first and hundred-th push cart on the image 3 (counting from the bottom)? There is infinite number of push-cars, on the image are depicted only first four. The mass of the bottom one is $m$, the second is $m/2$ and the mass of the weight attached is $m/2$ as well. The next mass is $m/4$ and the weight is $m/4$ etc. Assume that the weights are connected to the cars and are not moving in horizontal direction relatively to the carts. The friction between carts is negligible.
2. Series 18. Year - 3. helicopter
For helicopter to levitate it needs motor of power P. What is the power P' of the helicopter, which is scale copy of the previous one in scale 1:2? Assume the effectiveness of the rotor to be 100%.
Úloha byla převzata z MFO v Kanadě.
1. Series 18. Year - 3. bricklayer
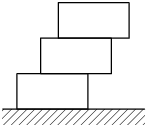
A bricklayer puts bricks as a stairs, one on each other. The aim is to build them as far as possible (horizontally) from the point where he started (where bricks are touching the ground). Suggest the strategy, which will give the longest reach! And, of course, no mortar/glue is allowed.
Navrhl Jarda Trnka.