Search

Test tubes of volumes 3 ml and 5 ml are connected by a short thin tube in which we can find a porous thermally non-conductive barrier that allows an equilbirum in pressures to be achieved within the system. Both test tubes in the beginning are filled with oxygen at a pressure of 101,25 kPa and a temperature of 20 ° C. We submerge the first test tube (3 ml) into a container which has a system of water and ice in equilbrium inside it and the other one (5 ml) into a container with steam. What wil the pressure be in the system of the teo test tubes be after achieving mechanical equilibrium? What would the pressure be if it would have been nitrogen and not oxygen that was in the test tubes?(while keeping other conditions the same)/p>

How quickly on average does water flow through the Gibralatar Strait if it allows the changing of high and low tide in the Mediteranean Sea? Find the required data on the internet and don't forget to cite them properly!

Take an empty cylindrical cup. Turn it upside down and push it beneath a calm water surface. How high will the column of air in the cup be depending on the submersion of the cup?

A hot air balloon with its basket weighs $M$. The basket of the baloon is submerged into a water reservoir and water flows into it. Now we shall raise the temperature a bit and by that we raise the buoyant force acting on the balloon $Mg+F$. The basket has the shape of a rectangular cuboid with a square base which has a side of size $a$ and is submerged into a depth $H$. The openings in the basket make up $p≪1$ of the whole area of the basket about which we assume that it is empty (with the exception of water). Let us neglect the viscosity of water and the volume of the basket itself. How quickly shall it rise depending on the depth of submersion?

Bonus: When shall it emerge?

Tip The expected speed of water flowing from the basket above the water surface is 2/3 of the maximum speed of water flowing out.

Each liquid has its specific viscosity. Try to make an Ostwald viscometer (capillary viscometer) and measure the relative viscosity of a few (at least three) liquids compared to water. Compare your results with what you find online.

A truncated cone that is the upside down (the hole is open downwards) may be held in the air by a stream of water which originates from the ground with a constant mass flowrate and an intial velocity $v_{0}$. At what height above the surface of the Earth will the cone levitate ?

Bonus: Explore the stability of the cone.

A horizontal pipeline with a flowing liquid contains a small bubble of gas. How do the dimensions of this bubble change when it reaches a narrower point of the pipeline? Can you find some applications of this phenomena? What problems could it cause? Assume that the flow is laminar.

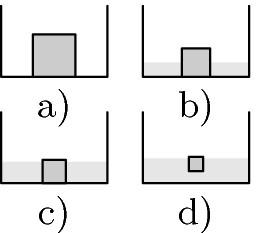
Large ice cube placed at the bottom of an empty pool starts to dissolve. Assume that the process is isotropic in the sense that the cube is geometrically similar at all times. What fraction of the cube needs to dissolve before it starts to float in the water? The surface area of the pool floor is $S$, and the length of an edge of the cube before it started disolving was $a$.

Imagine a large tank containg tea with a little opening at its bottom so that one can pour it into a glass. When open, the speed of the flow of tea from the tank is $v_{0}$. How will this speed change if, while pouring a glass of tea, someone is filling the tank by pouring water into it from its top? Assume that the diameter of the tank is $D$, the diameter of the flow of tea into the tank is $d$, and that of the flow of tea out of the tank is much smaller than $D$. The tea level is height $H$ above the lower opening, and the tank is being filled by pouring a water into it from height $h$ above the tea level. You are free to neglect all friction.

Estimate how much energy would be needed to evaporate all oceans (on Earth).