Search

Using dimension (unit) analysis find the relation for the speed of waves on the water surface. Verify the theoretical relation and find unknown constants from measuring the speed of waves dependent on wavelength. Do not forget that there are two types of waves – one caused by gravitational field and second by surface tension.

Explain why the tea in the box after it is shaken is separated such that larger pieces of tea leaves are on the surface. The solution can be enhanced using your observation.

Estimate the height of the trees on the planet. Think over all possible aspects influencing the height of the trees.

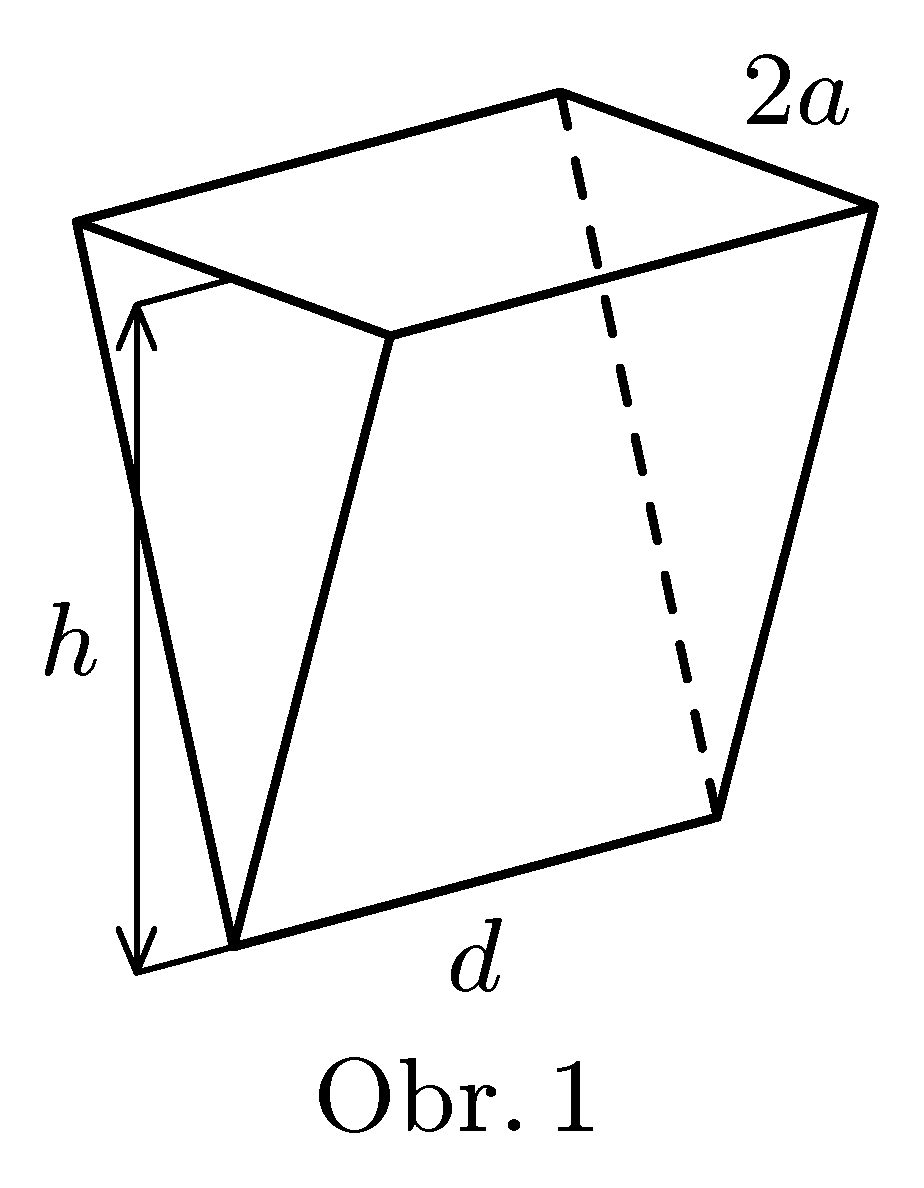
Scientists in NASA discovered special sediments of vegetable origin at Europa (Jupiter's moon). They are suitable for making very strong planks of oblong shape or triangular shape and are ideal for building a ship of height $h$, length $d$ and width 2$a$ (see figure 1) Help: captain to decide for which range of densities of ocean it is safe to sail such boat.

Assume that planks have constant thickness and density $ρ_{m}$ and that the ship is hollow and has a deck. (discuss the case when the ship is not hollow and has constant density $ρ_{m}.)$ It is not necessary to show just one final equation, more important is practical recipe (including all required equations) how to make such calculations. Try to make it simple to understand and explain all approximations made.

This series of questions is dedicated to the research on the „planet of the balloons“.

This year balloons are competing in the 'The higher, the better' competition. Each balloon has a piece of string attached to measure his height. All balloons have the same parameters and noone of them have won yet.

The length density of string is 11 lufts per sprungl, density of atmosphere is 110101 lufts per cubic sprungl and the radius of each balloon is 10 sprungls and weight of balloon is 10 lufts. Every object in gravitation field of the planet increases its speed by 111 sprungls per temp. Calculate the maximum height which the referees will measure and how the balloon will move after reaching this height. Unlifted part of the string is laying freely on the ground. The competition happens at low altitudes, where density of atmosphere is approximately constant.

Hint: Sprungl, luft and temp are units used on planet of the balloons. Each balloon has maximum of 1 string attached.

Two balloons are fixed on a single string of length $l$. The string is threaded through a horizontal hollow tube of length $L$. Both balloons weight approximately the same, however one is slightly heavier.

The tube starts spinning around vertical axis. What is the optimum position of this axis for the horizontal distance between balloons to be the biggest?

At the wedding ceremony the new couple kisses. For balloons it means to connect it orifices to connect the inside gas into a single One. Describe what would happened after the orifices are connected. Do not forget that all balloons have the same parameters.

Is it possible for the boat to move faster than the water in the river? Justify you answer and assume laminar flow.

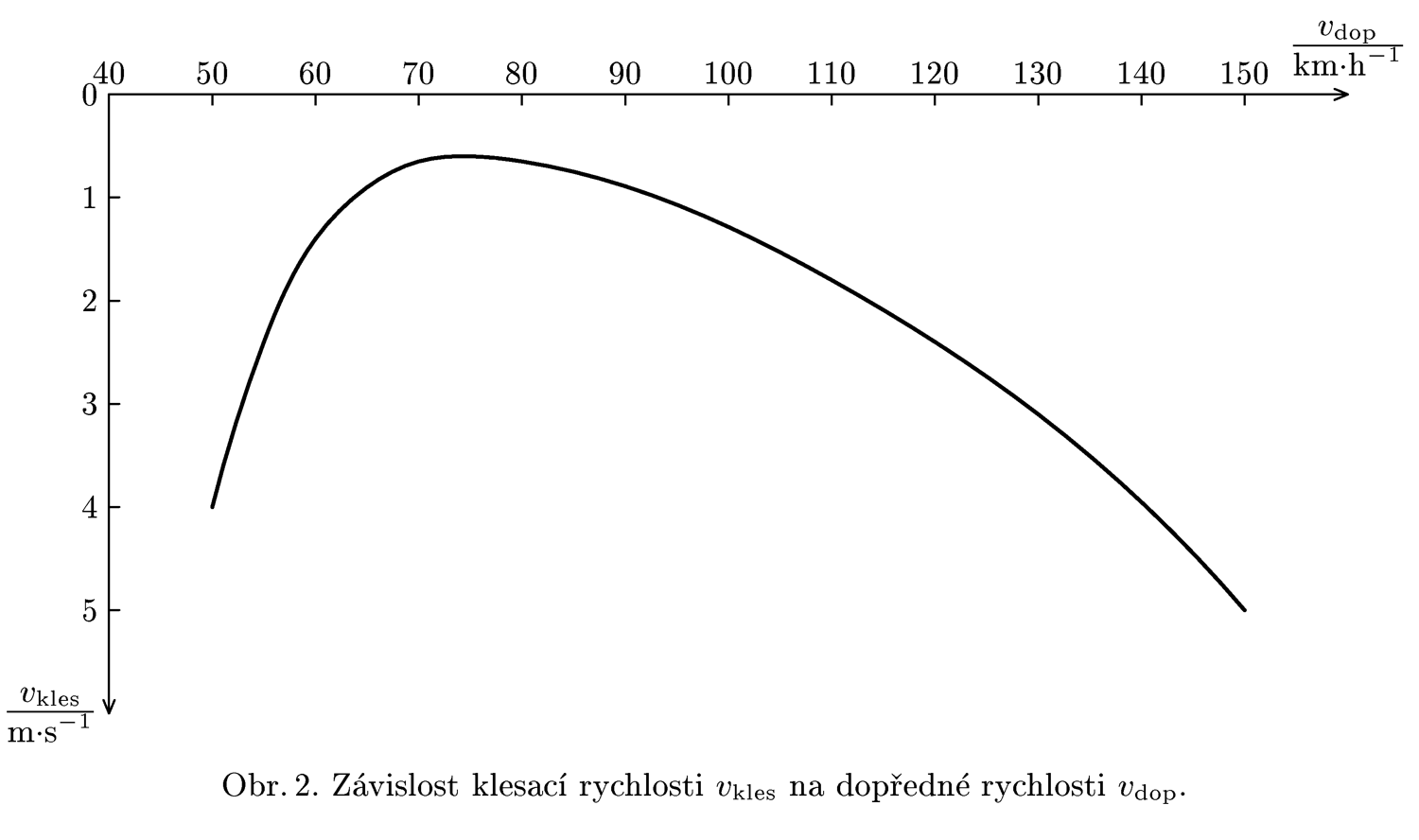
One of well known glider pilots decided to cross the British Channel. In Calais he rented a plane to took him to the height h = 3 km and from there glided directly to England. As every pilot knows, glider's downward speed $v_{kles}$ depends on the forward speed $v_{dop}$ as in the image 2. What is the optimum speed to achieve the longest flight? When the pilot is 3/4 of its way to England strong wind starts to blow in direction from England to France at the speed 10 $ms^{-1}$. What is the optimum speed now? What is the maximum wind speed which allows him to come to England? And what is the sped of wind to allow for the safe return to France?

Moses came to the Red Sea and said: „Lets the water open and let us go by dry foot to the land of promise.“ Then he entered into waves and they opened. What was the Moses's force, if he moved Jews over Red Sea. Assuming the sea to be 1 wide and 20 deep.