Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
gravitational field
(3 points)3. Series 31. Year - 2. small acceleration, large acceleration
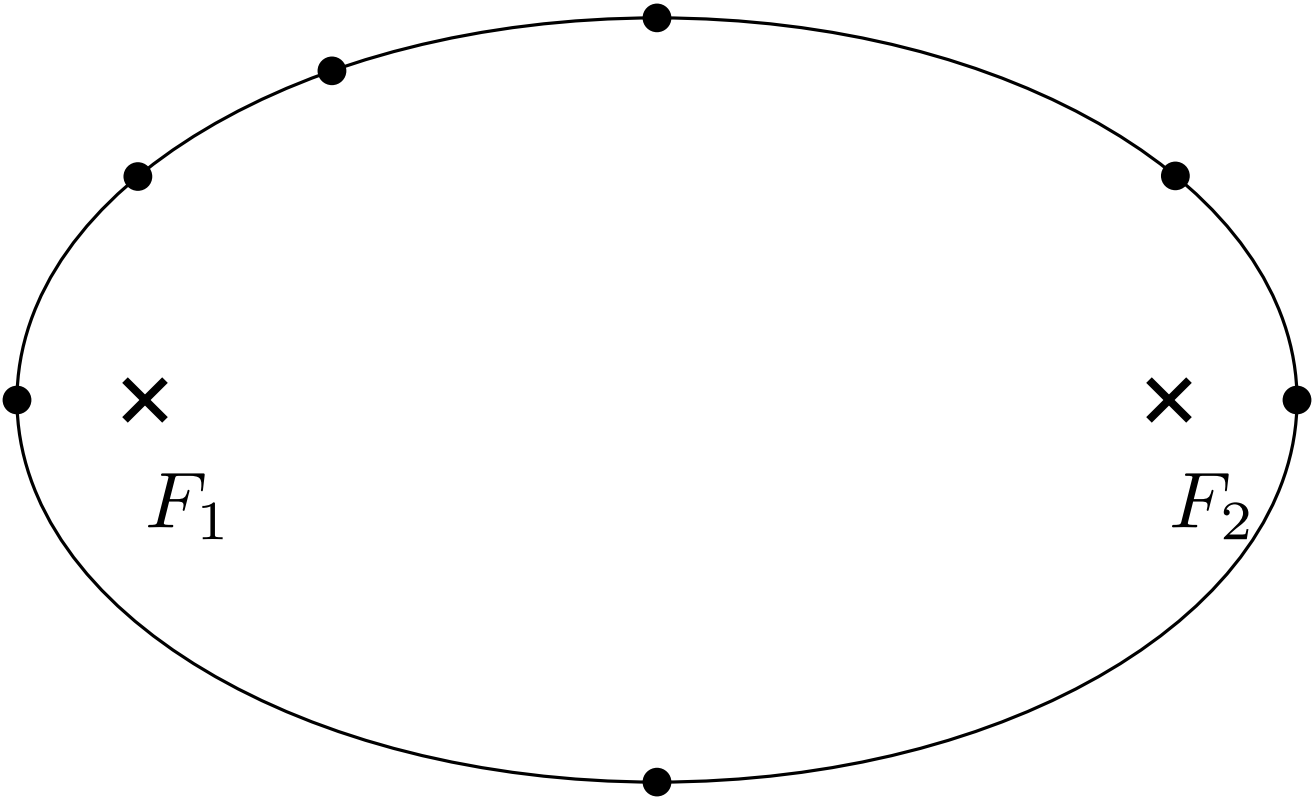
The ellipse
In the figure, there is an ellipse with two focal points $F_1$ $F_2$ and several marked points on the ellipse. The ellipse represents a trajectory of one material point. Plot the accelerations the point experiences in given points of its trajectory. Show it in a figure. The direction and ratio of accelerations are important.
- There is a massive body in the focal point $F_1$. The material point is orbiting it, and Kepler's $2^{\rm nd}$ law applies.
- The absolute value of velocity of the material point is constant. It only moves along the ellipse.
(3 points)6. Series 30. Year - 2. accidental drop
From what height would we need to „drop“ an object on a neutron star to make it land with a speed 0,1 $c$ (0,1 of speed of light). Our neutron star is 1.5 times heavier than our Sun and has diameter $d=10\;\mathrm{km}$. Ignore both the atmosphere of the star and its rotation. You can also ignore the correction for special relativity. However, do compare the results for a homogenous gravitational field (with the same strength as is on the star surface) and for a radial gravitational field. Bonus: Do not ignore the special relativity correction.
Karel was thinking about neutron stars (yet again)
(3 points)5. Series 30. Year - 1. space snowman
Consider a snowman consisting of 3 homogeneous spheres of density $ρ$ with centres on a line, floating in free space. The smallest sphere (the head) has radius $r$ and each consecutive sphere has twice the radius of the previous one. Our snowman is the only thing in the universe and it does not rotate in any way. Find the force holding the head to the rest of the snowman.
Bonus: Generalise the problem for $N\ge3$ spheres. Will the force converge to a finite value for $N→∞$ or will it go to infinity?
Karel came up with a problem for Fyziklani and realized he wouldn't want to be checking result.
(12 points)1. Series 30. Year - E. Pechschnitte
Does bread always falls on the side that has the spread on it? Explore this Murphy's law experimentally with emphasis on statistics! Does it depend on the dimensions of the slice, or the composition and the thickness of the spread? Try to explain the experimental results with a theory. Use a sandwich bread.
Terka má stůl ve špatné výšce.
(8 points)1. Series 30. Year - P. The sky is falling
Did you ever think about, why the clouds simply don't fall down, when they consist of water, which is much denser than air? The raindrops fall to the ground in minutes, so why not clouds? Try to physically explain this. Support all of your claims with calculations.
Mirek se zadíval na nebe a dostal strach.
(8 points)6. Series 29. Year - E. Malicious coefficient of restitution
If we drop a bouncing ball or any other elastic ball on an appropriate surface, it starts to bounce. During every hit on the surface some kinetic energy of the ball is dissipated (into heat, sound, etc.) and the ball doesn't return to its initial height. We define the coefficient of restitution as the ratio of the kinetic energy after and before the hit. Is there any dependence between the coefficient of restitution and the height which the ball fell from? Choose one suitable ball and one suitable surface (or several if you want) for which you determine the relation between the coefficient of restitution and the height of the fall. Describe the experiment properly and perform a sufficient number of measurements.
(6 points)6. Series 29. Year - P. iApple
Think up and describe a device that can deduce its orientation relative to gravitational acceleration and convert this information to an electrical signal. Come up with as many designs as you can. (An accelerometer-like device that is in most smart phones.)
(3 points)2. Series 29. Year - 3. fatal fall
From a spaceship on a circular orbit with height $h=2000\;\mathrm{km}$ above the surface of Earth a screwdriver is thrown with speed $v=5\;\mathrm{km}\cdot h^{-1}$ relative to the rocket towards the center of the Earth. Determine when will the screwdriver hit the surface?
Karel nemá rád šroubováky.
(8 points)1. Series 29. Year - E. small g
Measure the local gravitational acceleration with at least two different methods. Then compare these two methods in detail.
Viktor heard the complaint of the participants that they don't want to constantly be knee deep in water.
(5 points)6. Series 28. Year - 4. Unbearable weight
Before the edge of Discworld was reached and overcome and scientific expeditions were made to confirm the existence of the four elephants, turtle and determine its gender some primitve tribespeople thought that the force that kept them on the surface was due to a disc made from a superdense Wasneverwasium. It was truly a very primitive idea because as we know today the expedition, that confirmed the turtle's existence, infamously ended when its boat tore apart and fell or rather did not fall;… Nevertheless we would be interested what kind of surface density would such a disc have to if an object in its middle should experience, while neglecting magical forces, attracted with the same force as the gravitational force on Earth. Assume that, as the legends told, the disc is very thin and is placed ;$H=8^{4}m=4096\;\mathrm{m}$ under the surface of Discworld. The Disc should be hmomogeneous and the masses of other bodies negligible. Neglect the movement of the turtle and the elephants. If you haven't read the works of a genius for whom Death came recently then just replace Discworld with Earth. Discworld has a diameter of precisely $d=10000\;\mathrm{km}$ for our purposes.
Karel likes gravity