Search
astrophysics (85)biophysics (18)chemistry (24)electric field (71)electric current (76)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (72)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (155)wave mechanics (51)
mechanics of a point mass
4. Series 24. Year - 2. To the Sun
Karel has decided to throw his notes into the Sun. Help: him calculate the necessary initial velocity of his notebook so that it reaches the Sun. You can neglect the frictional froces acting on his notebook and you can also assume that the trajectory of the Earth around the Sun is circular. You know the masses of the Earth and the Sun as well as the distance of the Earth from the Sun.
Karel
1. Series 24. Year - E. shot put
We all know that in vacuum if we throw an object under a certain angle and with some initial speed the distance it will travel is independent upon the mass of the object. If we drop the vacuum assumption, the problem is not so simple. Experimentally find how does the distance of the point where the object hits the ground depends on its mass and shape. Make theoretical predictions (numerical calculations are allowed) and compare them with your findings.
1. Series 23. Year - 3. adiabatic invariant
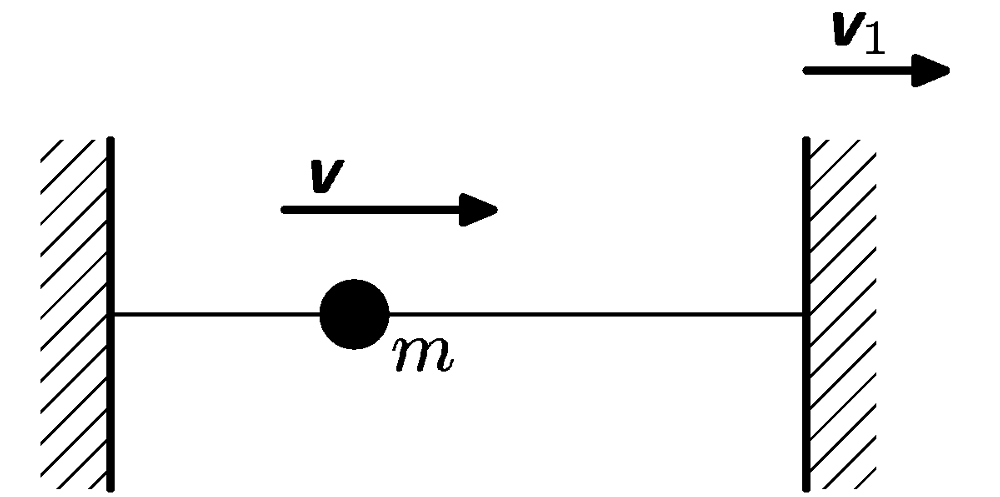
The movement of point mass is restricted on straight line by 2 end points. At the beginning the point mass $m$ is moving at speed $v$. The end point starts to move away at speed $v_{1}<<v$. How will the energy of point mass change?
Na Zajímavé teoretické fyzice nespala Janap.
3. Series 22. Year - 2. trainstopping
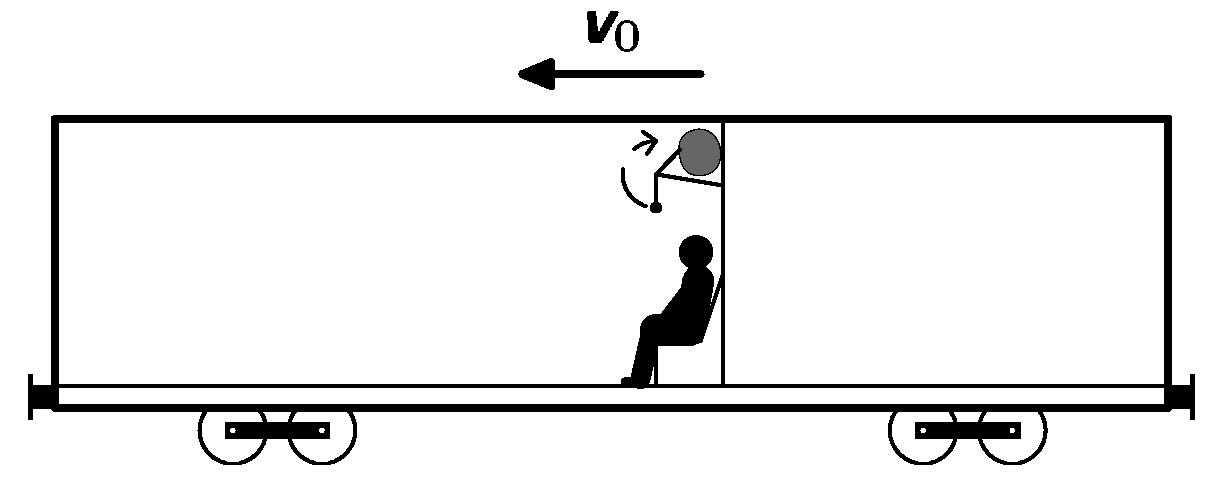
Honza travels home by train at speed $v_{0}$. From his baggage on top shelf is hanging down a mathematical pendulum. The train starts suddenly to break (at acceleration $a$ for duration $t)$. Can the pendulum go around of 180 °? Assume, that pendulum is fully fixed above.
Z maďarské přípravy na FO od Dalimila vybral Aleš.
2. Series 22. Year - 3. two balls
A small ball is at rest on bigger ball. The bigger ball is laying on the table without friction. We give a small impulse to the small ball and its will fall on the table. How far from the the original contact between table and large ball it will touch the table?
na teoretické mechanice zkoulel Lukáš Ledvina
2. Series 22. Year - E. slanted PET bottle
How much of water has to be inside PET bottle placed upside down onto cap to make it the most stable (stability is defined as at small inclination bottle will fall in longest time). Do not forget to make theoretical assumption.
nad vypitou lahví se zamyslel Béda
1. Series 22. Year - 1. sliding and oscillations
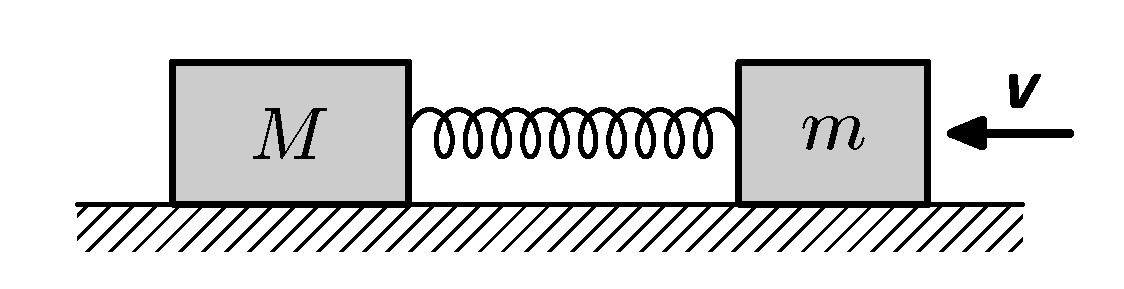
Two weights of masses $m$ and $M$ are connected by a spring of stiffness $k$ and lies on flat smooth surface (friction can be neglected). Body of mass $m$ gets velocity $\textbf{v}$ (see picture). What will be the smallest distance between the bodies? And when it will be reached?
V ročenkách kanadské FO našel Honza Prachař.
6. Series 21. Year - 1. free fall of Fykos-bird
A Fykos-bird (the symbol of the seminar) is flying 1 km above the forest at speed 4 m ⁄ s. It is shooted by a men with a gun. The bullet leaves gun at speed 710 m ⁄ s. Our men saw the bird just above his head and fired. How far from him the body of bird will touch the ground? Air friction is negligible.
Vyplodil Honza Prachař.
6. Series 21. Year - 4. quick retreat
Fykos-bird is running through a coridor, which is turning to left. The width of coridor is $b$, bird is running at speed $v_{0}$ and the turn is in distance $d$. If the acceleration will be bigger than $a_{0}$, it will slip and fall down. What is the optimum trajectory to have smallest possible delay?
Napadlo Honzu Jelínka při dobíhání tramvaje za rohem.
5. Series 21. Year - 2. question of survival
The entrance and the internal surface are connected by a ladder. You have already descended one kilometer, when you slipped and are falling down. What will be the speed you will fall down on Rama surface? How long it will take? Is there a chance to survive?
Martin Formánek