Search

A truck traveling at constant speed $v$ is carrying bottles of beer. The driver suddenly discovers a dangerous curve on the road in distance $d$ in front of him. The radius of curvature is $R$. What is the ideal tactic for slowing down, if the number of broken bottles is proportional to the maximum acceleration and you want this number minimised?

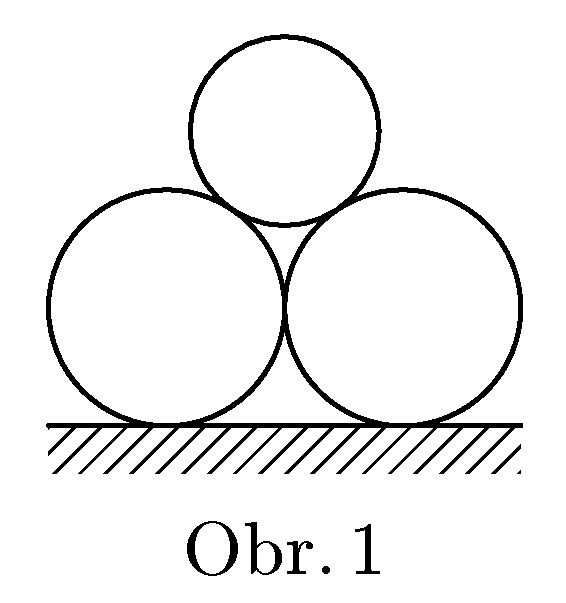
Find the condition of equilibrium (no movement) for the 3 cylinders in figure 1. The cylinders are made of material of density $ρ$, the radius of bottom cylinders is $R$, the radius of top cylinder is $r$. The coefficient of friction is same for all surfaces.

Diary of captain Kork: Star time 51824,2. Future of Star flotilla is endangered again. Romulan's are trying to destroy us, they are attacking us using battleship Karusel equipped with rotating laser gun. Doctor Spok decided that the direct contact is impossible and therefore we have to move as far as possible from the enemy battleship.

However we have no available scientist on the board and you have to figure out how to make a manoeuvre to escape the enemy. Our space ship Enterprise has spherical shape of diameter $R$, at beginning is at distance $r_{0}$ from enemy ship. The laser gun of Karusel is rotating at angular speed $ω$. The laser gun works also as a detector of targets (us), and after detectiong the target it fires in the same direction as the target was seen. What is the minimal speed our ship has to have in order to escape to safety?

Buffalo Bill is searching for Jessie James, well known bandit. Finaly he found him and in town Clay County they meet in fighting. Buffalo noticed a barrel full of petrol located in between both of them on a trolley. But how to get barrel near to Jessie (to light it up)?

Jessie made a hole in the barrel with his gun in 9/10 of height and the petrol is flowing from the barrel. Buffalo hits the barrel exactly in the middle and shoots again. Calculate what is the acceleration of the barrel and trolley at the beginning and how it depend on the position of the second hole from Bill's revolver. Assume the mass of bullet is negligible.

What height is optimal for petrol to splash to longest distance?

You may remember buying plastic bottle of your favourite drink in supermarket. The bottle placed on the belt starts spinning trying to stay on the spot. Why this happen?

Analyse following situation: the bottle in rest is placed on the belt perpendicularly to the direction of belt movement.

Suddenly the belt starts moving at constant speed $v=10\;\mathrm{cm}/s$. What will be the speed of the bottle. First analyse following idealisations: (1) approximate bottle by a solid cylinder, (2) the bottle is full of liquid water which does not like to be turned. For simplicity assume negligible viscosity, then include viscosity to your calculations.

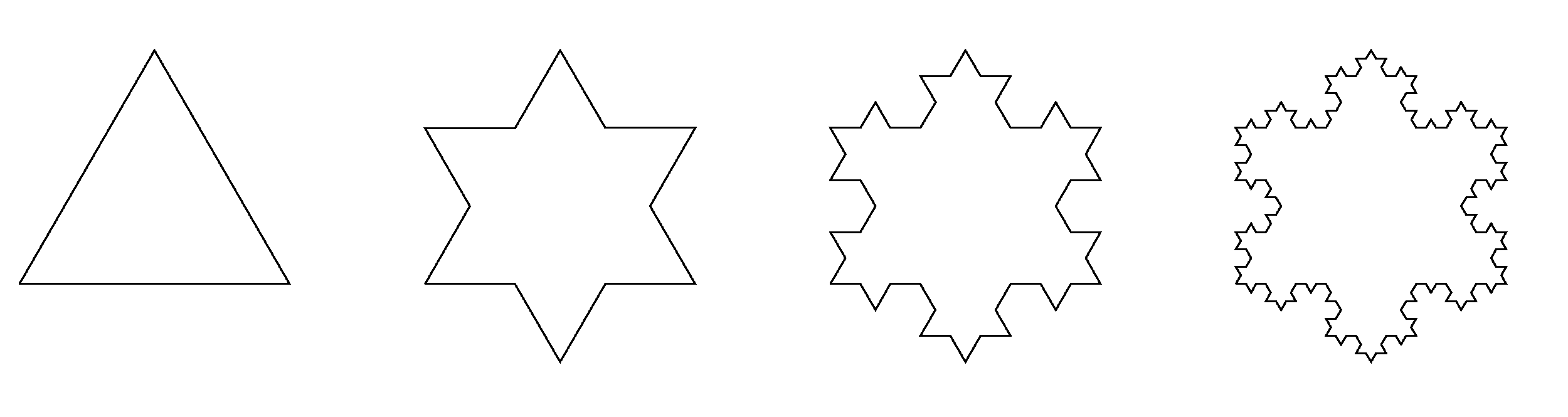
Calculate the moment of inertia of Koch's flake made from homogeneous sheet with respect to the axis going through the center of flake perpendicular to the paper. Assume the mass of flake to be $m$ and radius $a$.

Hint: Koch's flake is a shape created by iterative process of connecting equilateral triangles each three times smaller than previous to the previous object (see picture). The diameter of Koch's flake is distance of vertices on the opposite sides.

Measure dependence of sliding friction between two materials (pick your own) as it depends on the surface of friction force and mass of the body. Do not forgot to describe exact experimental configuration.

The space probe Huygens (named after the discoverer of Titan) has landed on Titan on Friday 14th of January 2005. The mother ship Cassini was travelling 7 years to reach Saturn. It is the most distant landing of man-made probe in history.

The landing module of nett weight (without fuel) $m$, equipped with reactive engine, levitated at fixed position above the surface of the moon (gravitational acceleration is $g)$. The module had available fuel of mass $M$ and energy $E_{0}$ which is used to accelerate the fuel (the speed and amount of fuel which is ejected from the engine can be regulated without any limitations). What is the maximum time the module can stay in constant height? Suggest how the speed and amount of fuel should be programmed to reach this maximum time.

Olympic discipline freestyle skiing (or acrobatic skiing) seems to contradict basic law of physics. Skier first speeds up and then comes on to jump ramp. Between take-off and landing he manages to make several flips and turns. Explain how and what he must make in order to spin in the way he wants and spectators expect. How would you falsify following opinion: „according to the momentum conservation law the skier must remain at rotation along the same axis at constant speed“.

Calculate the angle between asteroid's velocity and space ship's velocity after collision. Before the impact the spherical asteroid had same mass as the ship. Assume that the ships has spherical shape.