Series 5, Year 25
Upload deadline: -, CET
(2 points)1. the flu pill
Some pills against flu dissolve in water making it to fizz. At first the pill is on the bottom of the glass but after a while it rises to the surface. Why?
Lukáš wanted to avoid the flu.
(2 points)2. electric equilibrium
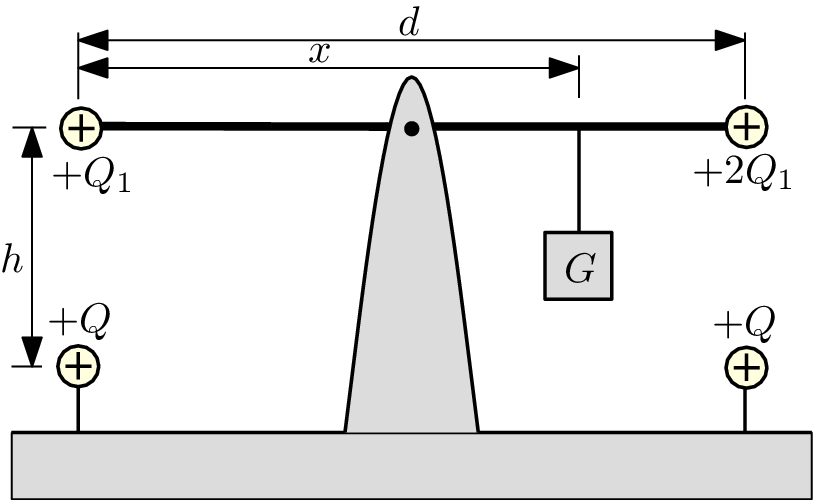
An insulating rod of length $d$ and negligible mass can rotate around its middle point (see picture). There are small balls of negligible mass and charges $Q_{1}$ and 2$Q_{1}$ on both of its ends. Due to the weight $G$ (see picture) the system is in mechanical equilibrium. Distance $h$ under each of the small balls is a another ball with charge $Q$.
- What is the distance $x$ for which the rod is horizontal and is in equilibrium?
- What is the distance $h$ such that the rod is in equilibrium but there is no force on the pivot that holds it?
Dominika dug into old problem sets.
(3 points)3. pilgrimage of pharaohs
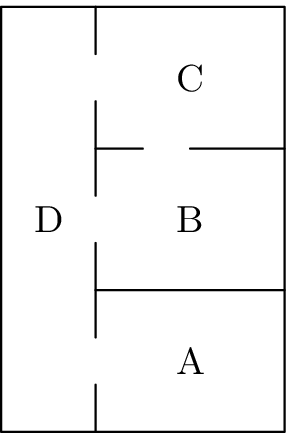
Mára decided to infect Aleš's four room apartment with pharaoh ants (top view of the apartment is on the picture). Ants are running all over the place but you can assume the following model of their motion. Every five minutes 60$%$ of ants in each room moves to the neighboring rooms and the rest stay where they are now. If there is more than one neighboring room assume that the same amount of ants moved to every one of them. This process repeats itself every five minutes (yes, assume only discrete time). The ants cannot move in or out of the apartment and they are immortal.
- If Mára places 1000 ants into the hallway (D) how many ants will be in each of the rooms after 5, 10 and 15 minutes? (2 body)
- If at some point we found out that the distribution of ants in the rooms is $N_{A}=12$, $N_{B}=25$, $N_{C}=25$ a$N_{D}=37$, how where they distributed 5 minutes earlier? (1 bod)
- *Bonus:** How would they be distributed after essentially infinite time if we start with 1000 ants in the hallway again? Does it matter how where they distributed in the beginning? And finally - will the distribution of ants in the rooms reach a stationary value or will it oscillate? (bonus points)
Karel studied Jordan form of a matrix.
(5 points)4. mother and a stroller
Mother is connected to a stroller of mass $m$ with a string of length $l$ that is initially fully stretched. The coefficient of friction between the floor and mother resp. stroller is $f$. Mother starts pulling the stroller with constant velocity $v$ that is perpendicular to the initial orientation of the string. Describe the dependence of the trajectory of the stroller on system parameters. Assume both the mother and the stroller have negligible size. We recommend that you numerically simulate this problem.
final exam
(4 points)5. hunter v2
How much should we increase the power output of train's motor per one caught bird per second if we catch the birds in a net placed on top of the car? Train moves with speed $v$, bird's mass is $m$, his speed $w$, the angle with which the bird hits the net is $φ$ and the net has area $S$. Assume that after each catch the net returns to its initial shape.
Organizers took the train.
(5 points)P. lightsaber
Design a lightsaber that looks and works in a similar way as the ones from Star Wars movies but using only knowledge and technology available to us.
Remembering old FYKOS camps.
(8 points)E. sweet coffee
Together with this problem set you also received a bag with sugar or sweetener. Your task is to experimentally compare „sweetness“ of this sample with other kinds of sugar/sweeteners. You should use the attached spoon as a measure of volume. „Sweetness“ of a sample is determined from a solution of one leveled spoon of the sample in 1 dl of water. As a reference point of „sweetness“ you can use for example refined beet sugar. You should determine „sweetness“ by comparing solutions of tested samples with the reference sample. To make the measurement more valid you should ask other people to rate the samples as well. For every sample find out its composition and report your results in an appropriate way.
Hint: The regular sugar is usually refined beet sugar, but you can also get cane sugar (almost the same in composition as beet sugar), grape sugar (dextrose) and fruit sugar (fructose). Examples of sweeteners are sorbit, huxol, sucralose or aspartame. You can also use honey. We recommend to use sugars/sweeteners with similar „sweetness“. If this is the first time you participate in FYKOS just send us an email to podezrelyprasek@fykos.cz and we will send you your sample. Warning Every substance can be dangerous in large amounts. Even distilled water is a poison. Try not to exceed recommended daily doses.
Karel has a sweet tooth.
(6 points)S. serial
- Active galaxies appear as a point sources, same as stars. Try to find some ways to distinguish between star and AGN. The more ways, the better.
Radio observations of quasar 3C 273 showed that there's a blob of radio emission moving away from the nucleus with angular velocity μ = 0.0008 year^{ − 1}. Assuming the radio knot is moving perpendicular to the line of sight, and using the distance $d=440/hMpc$, where $h$ is Hubble constant, compute apparent velocity $v_{zd}$.
- Derive for which value of angle $φ$ is $β_{T}$ maximal?
- Let's assume that the supermasive black hole in the galactic centre is 30 % efficient. How much energy will the hole produce when swalloving an Earth size