Serial of year 18
You can find the serial also in the yearbook.
We are sorry, this serial has not been translated.
Tasks
1. Series 18. Year - S. kinematics of point mass
* The position of point mass in time in Cartesian coordinates is described by position vector $\vect{r}(t) =(R \cos\(\omega t\)$,R sin\(\omega t\),d)\,.$$ Calculate, what is time dependence of vectors $v(t)$ and $a(t)$. Calculate tangential, normal and bi-normal component of acceleration.
- A wheel of radius $R$ rolls without slipping at straight track at velocity $v$. A point is connected with the wheel at the distance $r$ from the centre of wheel. Calculate its movement and the velocity as function of the time in coordinate system connected with the Earth. Can the speed be zero at some moment?
Autoři seriálu.
2. Series 18. Year - S. Newton's kinematics equations
- Write down and solve the kinematics equation for mass point in gravitation field of the Earth. The orientation of the coordinate system make that $x$ and $y$ are horizontal and z is vertical, pointing upwards. The starting position is $\textbf{r}_{0} = (0,0$,$h)$, starting velocity is $\textbf{v}_{0} =(v_{0}\cosα,0,v_{0}\sinα)$.
- The man with the gun sits in the chair rotating alongside vertical axe at frequency $f=1\;\mathrm{Hz}$. With the chair also the target is rotating (it is fixed to the chair). Then the man shoots the bullet at the speed of $v=300\;\mathrm{km} \cdot \mathrm{h}^{-1}$ from the rotational axes directly to the middle of the target. In what place the bullet is going to go through the target. Solve in non-inertial system and from the inertial system. The distance to the middle of the target from the centre of rotation is $l=3\;\mathrm{m}$, the air friction is negligible.
- State the dependence of the speed of the mass point at its position in gravitational field of the Sun.
Zadal Honza Prachař.
3. Series 18. Year - S. Langrange's equations first type
- Lets have a mass point suspended on massless string. Introduce Cartesian coordinates and write down equation for the mass point.
- Write Lagrange's equations of first type for mass point from part a). Show, that they are equivalent with the equation for mathematical pendulum
d^{2}$\varphi/dt^{2}$ + $g/l$ \cdot sin $\varphi$ = 0,
where $\varphi$ is angular displacement from equilibrium.
- Small body is in rest at the top of the hemisphere and starts to slide down. Using Lagrange's equations for first type calculate the height when the body take-off the hemisphere. (
Hint: The body takes-off when the $λ$ = 0.)
Autoři seriálu.
4. Series 18. Year - S. Lagrange equation of the 2nd type
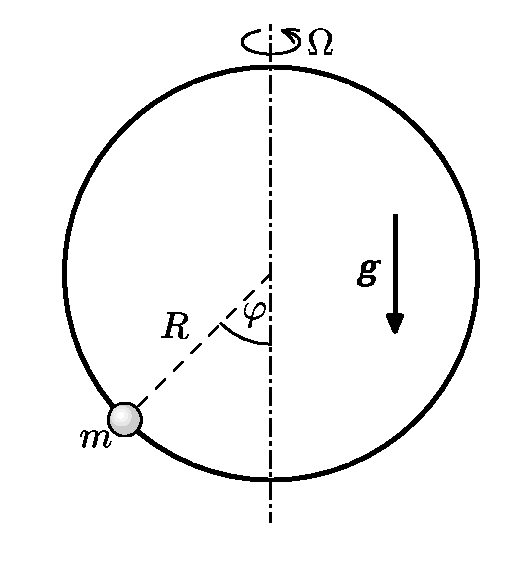
The small bead of the mass $m$ is sliding without friction on the wire loop of the shape of circle of radius $R$, the loop is rotating with the constant angular speed $Ω$ around the horizontal axis (see image).
- Select appropriate generalised coordinate and construct Lagrange function of the problem.
- Construct Lagrange equation of the 2nd order which describes the motion of the bead.
- Decide, when the equilibrium position in the lowest point of the loop stable and unstable, depending on $Ω$. For $Ω$, when this position is stable calculate the period of the oscillations of the bead around this stable position.
- For a bonus point find next stable equilibrium positions and discuss if they are stable or unstable. For stable equilibrium positions calculate frequencies of oscillations.
Navrhli autoři seriálu Jarda Trnka a Honza Prachař.
5. Series 18. Year - S. Mercury, the pit and the pendulum
The following questions will test the knowledge from all presented chapters about mechanics – Newtons formalism, D'Alembert's principle and Lagrange's formalism.
- Imagine planet Mercury orbiting around Sun. It is know, that its elliptic trajectory is rotating, the position of perihelion is moving, which cannot be explained by gravitation force.
$\textbf{F}=κ(mM\textbf{r})⁄r^{3}$.
Proof, that adding an additional central force
$\textbf{F}=C(\textbf{r})⁄r^{4}$,
where $C$ is suitable constant, full trajectory (ellipse) will rotate at constant angular speed. In other words, that exists a frame rotating at constant speed, where the trajectory is an ellipse. Knowing this angular speed $Ω$, calculate the constant $C$. Is such correction for gravitation enough?
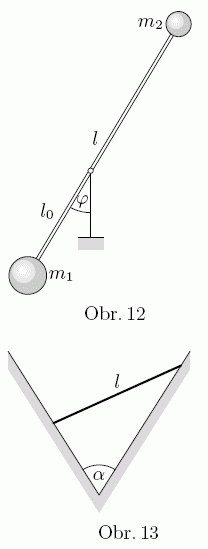
- Calculate equilibrium position of homogeneous rod of length $l$ supported by inner wall of excavation in the V-shape (see figure 12) as a function of the angle of V-shape $α$.
- Using Lagrange's equations calculate period of small oscillations of double-reverse pendulum in image 13. The weight are at the ends of weightless rod of the length $l$ and have masses $m_{1}$ and $m_{2}$, the distance from the joint from the weight $m_{1}$ is $l_{0}$.
a)Na úlohu narazil Matouš v jedné pěkné ruské knize. b), c) Zadal Honza Prachař a Jarda Trnka.
6. Series 18. Year - S. Hamilton formalism
Lagrangian of a particle in electromagnetic field is
$L=\frac{1}{2}mv-qφ+q\textbf{v}\cdot \textbf{A}=\frac{1}{2}\;\mathrm{m}\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,
where $φ$ is electrical potential and $\textbf{A}$ is magnetic vector potential.
- Calculate generalized momentum of the particle $p_{i}$ belonging to the speed $v_{i}$.
- Write Hamiltonian function (in variables ($x_{i}$, p$_{i})!)$.
- Solve Hamiltonian equation, if when $\textbf{A}=**0**$ and $φ=-Ex_{1}$.
Zadal Honza Prachař.